Гамма-распределение непрерывной случайной величины и его разновидность - распределение Пуассона непрерывной случайной величины.

Гамма - распределение относится по классификации Пирсона к третьему типу кривых, в этот тип входит обширная группа асимметричных распределений (в том числе и бета – распределение). Данные, которые подчиняются этим распределениям, никакими преобразованиями не могут быть преобразованы таким образом, чтобы после они имели нормальное распределение. Однако одна из разновидностей гамма - распределения имеет для нас значение, так как существуют способы преобразования данных, после которых они могут подчиняться логнормальному и нормальному распределению. Плотность вероятности гамма - распределения описывается следующей формулой

G (x;Γ;β) = x^r-1*e^-χ/β/ Γ(г) β^r x≥0, r >0, β>0.

Дополнительными параметрами гамма - распределения являются величины r и β, первый является параметром положения, а второй параметром масштаба.

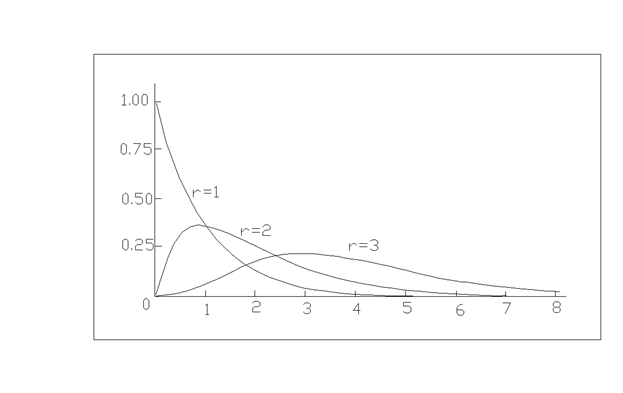
Рис Примеры кривых плотности вероятности, соответствующие различным значениям r, при β = 1.

Выбор гамма распределения в качестве модели распределения изучаемой совокупности определяется наличием у изучаемой кривой распределения так называемого хвоста, являющегося следствием асимметричности распределения и препятствующим различным математическим преобразованиям привести экспериментальные данные к нормальному или логнормальному распределению. Так же как и для нормального распределения плотности вероятности распределения, выраженные через площади под кривой распределения, давно рассчитаны и опубликованы в таблицах. Вычислить и оценить параметры - r и β можно по таблицам Сиддикуи и Вейса и через них рассчитать μ и σ² (то есть истинное среднее совокупности и ее дисперсию) по формулам

μ = β* r;

σ²= β²* r.

Как видно из этих формул, для гамма - распределений отмечается сильная зависимость между средним и дисперсией, тогда как в случае нормального распределения такой зависимости нет.

Основные компоненты полиметаллических месторождений, месторождений цветных металлов и золота могут подчиняться разновидностям гамма – распределения. Частным случаем, гамма распределений является распределение Пуассона, если его использовать для анализа непрерывных случайных величин. Особенно это распределение характерно для месторождений золота, так как именно в большей части на этих месторождениях часты находки самородков золота (редкие события) или можно перефразировать - встречаются пробы с аномальным высоким содержанием золота (ураганные пробы), во много раз превышающим наиболее распространенные содержания металла по конкретному месторождению (эффект самородков). Несмотря на то, что гамма - распределения, в том числе и распределение Пуассона хорошо изучены на практике, специалисты стараются не использовать эту модель для оценки истинных параметров изучаемой совокупности из-за ряда причин, в том числе и из-за сильной зависимости между средним и дисперсией. Для решения этой задачи общепринят иной подход, при котором эффект самородков стараются нейтрализовать и затем после возможных преобразований данных предположить нормальную модель их распределения и оценивать параметры исходя из нормальной модели распределения значений полезных и вредных компонентов месторождений.