Логнормальное распределение непрерывной случайной величины.

Одним из самых близких к нормальному распределению является логнормальное распределение, имеющее слабую левую асимметрию и относящееся ко второму типу распределений. Очевидно, что многие геохимические компоненты не подчиняются нормальному распределению, например концентрация селена в растительном материале, концентрация йода в грунтовых водах подчиняются асимметричным распределениям. Кривая логнормального распределения отражена на рисунке.

Существуют две физические причины асимметричности. Первая причина кроется в пороге чувствительности приборов, определяющих концентрацию редких химических элементов (селен, радий и др.). Левая асимметричность возникает, из-за того, что много данных концентрируется около порога чувствительности, и если бы этого порога не было, то распределение приняло бы нормальный симметричный вид.

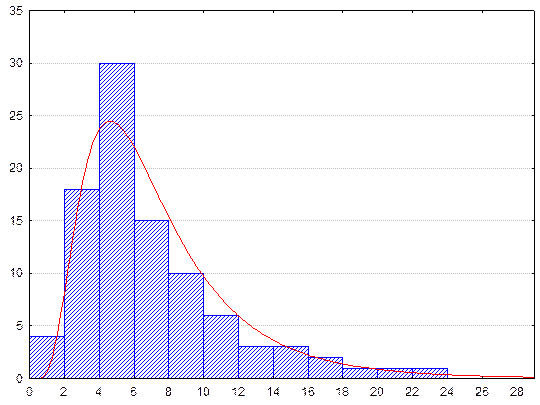
Рис. Кривая логнормального распределения.

Вторая причина кроется в детерминированности изменений природных объектов, тем более мощные геохимические и тектонические процессы, которые протекали при формировании залежей полезных ископаемых, тем более кривая распределения характеристик этих залежей будет асимметричной. Асимметричность, например, возникает, если толкать спортсмена-стрелка в тире в момент выстрела, в этом случае пули на мишени будут располагаться преимущественно с одной стороны мишени. Если результаты наблюдений, распределение которых представлено на рисунке, прологарифмировать (то есть вместо переменной x_i использовать переменную y = log x_i), то распределение прологарифмированной переменной примет нормальный вид. Все перечисленные ранее параметры и статистики также характерны и пригодны и для логнормального распределения. На практике они рассчитываются по тем же формулам, только предварительно все значения выборки логарифмируются, однако основные статистики можно посчитать, используя и не преобразованные данные, в этом случае среднеарифметическому значению будет соответствовать геометрическое среднее, а значению дисперсии будет соответствовать геометрическая дисперсия. Преобразования типа y = log x_i широко применяются в геологии, однако известно (У.Крамбейн, Ф.Грейбилл) и так называемое фи - преобразование - φ = - log x_i. Это преобразование используется, например, при изучении распределений размеров частиц осадочных пород.

Лекция 8.