Стандартизация переменных и таблицы плотности вероятности нормального распределения.
Закономерность распределения случайной величины (или случайной ошибки измерения), если распределение этой величины описывается нормальным законом распределения, достаточно хорошо изучена. Плотность вероятности нормального распределения определяют по формуле
φ(x) = [(1/σ)√2π]*e-(xi – μ)( xi – μ)/(2σ*σ) .
Часто вместо переменной xi используют нормированную переменную u, получаемую, используя следующее преобразование
u = (xi – μ)/σ.
Это очень полезное преобразование, называемое стандартизацией. В результате стандартизации среднее становится равным нулю, а стандартное отклонение равным 1. В результате такого преобразования все значения переменной измеряются в единицах стандартного отклонения от -3 до +3, со средним равным 0. В результате стандартизации переменные, первоначально измеренные в каких-либо единицах измерения, таких как кг, футы, см, проценты и другие переходят во внутреннюю систему координат с нулевым средним и становятся безразмерными, при этом сохранив соотношение между цифрами, как до преобразования. Стандартизация позволяет вместе анализировать переменные, измеренные в разных единицах измерения. После подстановки в формулу Гаусса мы получаем формулу плотности вероятности более простого вида
φ(x) = [1/ √2π]*e-(u*u)/2.
Плотности вероятности стандартного нормального распределения известны и давно рассчитаны, изданы таблицы, которые можно найти в любом учебнике по статистике и теории вероятности, в которых площади под кривой распределения прямо выражаются через вероятности.
Лекция 7
Рассмотрим пример.
На эксплуатационном блоке полиметаллического месторождения были отобраны пробы и получены данные, содержащиеся в таблице.
Данные были получены следующим образом. При подготовке блока к эксплуатации было пробурено 96 вертикальных скважин по квадратной сети 3.5 метра на 3.5 метра. Каждая скважина была опробована по интервалам (длина интервала -1 метр). Большое число равномерно расположенных в блоке проб позволило определить среднее содержание металла в блоке с большой точностью. Блок был разделен на 24 участка, в каждом из которых, оказалось, по 12 проб (4 скважины на 1 участок, 1 скважина содержит по 3 пробы). Общее количество проб равно 288 (24*12 = 288).
| Содержание (%) | Частота | Относительная частота (частость) |
| 0 – 0.5 | 0.205 | |
| 0.5 -1 | 0.389 | |
| 1 -1.5 | 0.202 | |
| 1.5 – 2 | 0.062 | |
| 2 – 2.5 | 0.042 | |
| 2.5 – 3 | 0.028 | |
| 3 – 3.5 | 0.017 | |
| 3.5 – 4 | 0.017 | |
| 4 – 4.5 | 0.007 | |
| 4.5 – 5 | 0.004 | |
| 5 – 5.5 | 0.007 | |
| Всего: | 1.00 |
На рисунке приведено распределение содержания металла в 288 пробах.
Как видно на рисунке распределение носит асимметричный характер и явно не подчиняется нормальному закону.
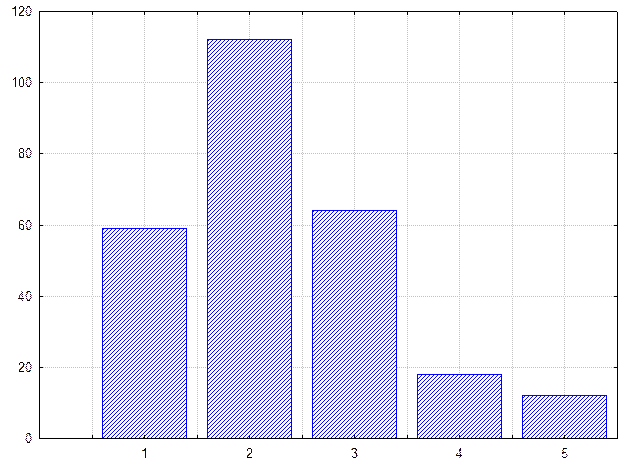
Рис. Гистограмма распределения полезного компонента в эксплуатационном блоке.
Затем было произведено 180 выборок из имеющихся анализов проб. В каждую выборку были случайным образом отобраны из каждого участка по одной пробе. Случайность отбора проб по участкам достигалась при помощи выбора свернутого листка с номером пробы из урны из общего количества свернутых листочков, равного количеству проб на участке. Для каждой выборки рассчитывалось среднее содержание металла, то есть в результате были получены 180 выборочных средних значений. Распределение выборочных средних значений по эксплуатационному блоку приведено в таблице и на рисунке.
| Содержание (выборочное среднее) | Частота | Относительная частота (Частость) |
| 0.7 – 0.8 | 0.017 | |
| 0.8 – 0.9 | 0.072 | |
| 0.9 – 1.0 | 0.167 | |
| 1.0 – 1.1 | 0.222 | |
| 1.1 – 1.2 | 0.228 | |
| 1.2 – 1.3 | 0.172 | |
| 1.3 – 1.4 | 0.089 | |
| 1.4 – 1.5 | 0.028 | |
| 1.5 – 1.6 | 0.005 | |
| Всего | 1.0 |
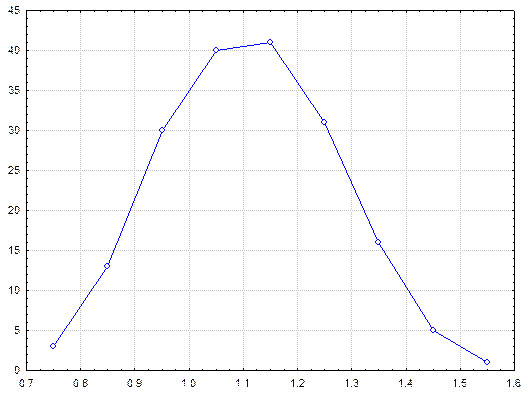
Рис. Распределение выборочного среднего значения по блоку.
Кривая распределения выборочного среднего значения похожа на колокол, причем среднеарифметическое всех выборочных средних значений равно 1.1, что соответствует среднему содержанию металла в блоке, которое как было уже указано выше, определено с большой точностью. Как видно из рисунка распределение выборочных средних значений соответствует или близко к нормальному распределению, хотя распределение просто полезного компонента имеет ярко выраженный асимметричный характер. Используя данные последней таблицы можно вычислить вероятность взятия пробы с некоторым содержанием или плотность вероятности, то есть вычислить вероятность взятия образца определенного класса. По данным второй таблицы вычисляем среднее и стандартное отклонение выборочных средних значений (χ = 1.11, а S = 0.159), а после для нижних границ по каждому интервалу вычисляем параметр u и получаем стандартизированные данные, у которых среднее арифметическое равно 0, а стандартное отклонение равно 1.
U1 = (0.8 – 1.11)/0.159 = -1.95
Далее берем таблицы вероятности нормального распределения и для u1 находим по таблице φ(x), в этом случае φ(x) = 0.026. Это также означает, что площадь части совокупности под кривой распределения, если смотреть по абсциссе, от минус бесконечности до значения u (u=-1.95), равна 0.026. Также вычисляем вероятности для класса, например для класса 0.8 – 0.9.
φ(0.8<x>0.9) = φ(u=-1.32) - φ(u=-1.95) = 0.093 – 0.026 = 0.067
То есть мы можем сказать, что с вероятностью 6.7% мы можем взять на месторождении пробу с содержанием от 0.8% до 0.9% данного металла.
Тот же самый результат мы получим, если расчеты будем делать не по таблице, а по формуле
φ(x) = [1/ √2π]*e-(u*u)/2.
Если мы, используя формулу или таблицу вероятностей нормального распределения, рассчитаем вероятности для всех значений u, то увидим, что они близки к частостям последней таблицы по классам, из чего можно сделать вывод, что распределение наших эмпирических данных соответствует нормальному распределению.
Обычно мы не знаем, из какой совокупности мы берем выборку, но очень часто подозреваем, что изучаемая совокупность явно значительно отличается от нормальной совокупности. Эти подозрения обычно обусловлены сильно выраженными геологическими процессами, проявившимися на конкретном месторождении. Нужно отметить, все случайные величины, которые мы получаем в результате измерений, делятся на стохастические и детерминированные величины.
Стохастические случайные величины изучаемых признаков характерны для обычных спокойных, длительных во времени геологических и геохимических процессов. Обычно распределение стохастических величин подчиняется нормальному закону распределения.
Детерминированные величины возникают в результате определенных направленных процессов в земной коре, например приводящих к аномально высоким концентрациям химических элементов на локальных участках, которые потом нередко определяются геологами как промышленные скопления полезных компонентов. Теоретически детерминированные изменения природных объектов могут быть описаны средствами точных наук - физики, химии и математики, но практически тектонические и геохимические процессы в большей части очень сложны для понимания и описываются геологами на уровне гипотез. В большей части случаев стохастические, и детерминированные величины перемешаны между собой. Распределение этих перемешанных величин может подчиняться нормальному закону распределения, но больше всего распределения этих величин имеют ярко выраженный асимметричный характер.
Согласно классификации Пирсона можно выделить три типа данных, которые имеют три соответствующих типа распределений. К первому типу относятся данные, имеющие симметричное нормальное распределение, ко второму типу относятся данные, которые после математических преобразований будут иметь нормальное распределение и к третьему типу относятся данные, которые при любых преобразованиях не будут иметь нормальное распределение.
Дата добавления: 2019-04-03; просмотров: 613;
