Среднее положение распределения.
Наиболее очевидная характеристика – это среднее положение распределения. Существует несколько видов среднего положения распределения, но только некоторые из них используются на практике.
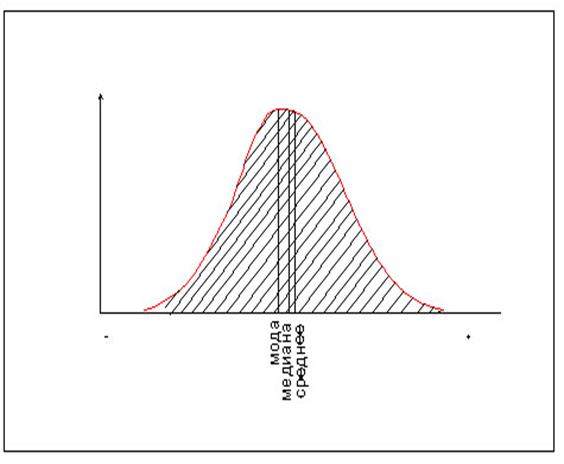
Рис. Соотношение моды, медианы и среднеарифметического на графике непрерывного распределения случайной величины.
Первая характеристика – это мода. В распределении, приведенном на рисунке, мода соответствует средней точке на оси абсцисс, находящейся под наивысшей точкой кривой частот и в принципе соответствует обиходному пониманию этого слова - мода. Модно то, что наибольшее количество людей на себя надевает и носит.
Моду можно рассчитать по следующей формуле:
Mo = xo +i*{(fmo-fmo-1)/[(fmo-fmo-1)+(fmo-fmo+1)]}
Где xo – нижняя граница модального интервала (модальным называется интервал, имеющий наибольшую частоту), i – величина модального интервала, fmo – частота модального интервала, fmo-1 , fmo+1 - соответственно частота интервала, предшествующего модальному и следующему за модальным.
Вторая характеристика – это медиана. Медиана соответствует средней точке на оси абсцисс, так перпендикуляр, проведенный через эту точку, делит площадь под кривой пополам, то есть половина площади от этой точки находиться справа, а половина находится слева. Главное свойство медианы заключается в том, что сумма абсолютных отклонений признака от медианы меньше, чем от любой другой величины. Медиану можно рассчитать по следующей формуле:
Me = xe +i* {[(1/2∑fi)- Sfme-1]/Sfme}
где xe – нижняя граница медианного интервала (медианным интервалом называется первый интервал, накопленная частота которого превышает половину общей суммы частот), i – величина медианного интервала, Sfme-1 – накопленная частота интервала, предшествующего медианному, Sfme – частота медианного интервала. (1/2∑fi – равна 50%).
И третья самая важная характеристика это точка на оси абсцисс, соответствующая среднеарифметическому значению, которое рассчитывается как сумма всех результатов наблюдений, деленная на их число.
χ=∑xi/n
Основной характеристикой центра распределения является средняя арифметическая, все отклонения от нее (положительные и отрицательные) равны 0, для медианы характерно, что сумма отклонений от нее по модулю является минимальной, а мода представляет значение признака, которое наиболее часто встречается. Соотношение моды, медианы и среднеарифметической позволяет оценить асимметрию распределения. В симметричных распределениях все три характеристики совпадают, чем больше расхождение между модой и среднеарифметической, тем больше асимметрия распределения. Для умеренно асимметричных распределений разность между модой и среднеарифметической в 3 раза превышает разность между медианой и среднеарифметической.
Mo– χ=3(Me – χ).
Моду и медиану легко определить графически. Мода определяется по гистограмме распределения и соответствует самой высокой точке кривой или середине самого высокого прямоугольника гистограммы (середине модального интервала). Медиана определяется легко по кумулятивной кривой гистограммы, на ординате находится точка, соответствующая 50% накопленных частот из которой проводится до пересечения с кривой графика прямая, параллельная оси абсцисс, затем из точки пересечения опускается до оси абсцисс перпендикуляр, который и указывает на значение медианы.
Многие символы традиционно используются для обозначения кривых распределения, обычно для теоретических распределений или распределений совокупностей традиционно используются греческие буквы, а для обозначения характеристик выборок используются латинские буквы. Так среднее выборки обозначают как χ, а теоретическое среднее или среднее всей совокупности обозначают как μ. Статистика, которую мы вычисляем по выборке, используется как оценка истинного параметра совокупности. Использование в качестве обозначения характеристик греческих и латинских букв подчеркивает разницу между параметрами и соответствующими им статистиками. Среднеарифметическое значение, вычисленное по выборке, имеет два очень важных свойства, которые делают его более полезным для оценки истинного среднего или центрального положения распределения совокупности, чем любая из оставшихся характеристик (медиана или мода). Во-первых, среднеарифметическое выборки, в которой все пункты наблюдения, в которых проводились измерения, или отбирались пробы для последующих исследований, выбирались случайно, чаще всего является несмещенной оценкой истинного среднего значения совокупности. Во-вторых, для нормального распределения (как симметричного распределения) среднеарифметическое значение выборки характеризуется тенденцией лучшего приближения к истинному среднему или к среднему значению совокупности, чем медиана, посчитанная по той же выборке. Однако медиана нередко является лучшей оценкой среднего совокупности, когда мы имеем дело с асимметричными распределениями, когда результаты измерений не подчиняются нормальному распределению. Медиана позволяет в этом случае дать более объективную оценку среднего положения для большей части совокупности (до 99%), но не для 100 % совокупности.
Среднеарифметическое значение совокупности μ называют математическим ожиданием. Математическое ожидание определяется как сумма произведений всех возможных значений случайной величины на их вероятности:
μ= ∑xi*pi (pi – вероятности появления значений случайной величины).
Эту формулу легко понять, так как среднеарифметическое значение рассчитывается как:
χ= (x1*m1 + x2*m2 …….xn*mn)/n = ∑xi*(m/n)
где xi - это значения переменной, n – это общее количество данных, m – это количество значений переменной, а так как частота (m/n) появления события при увеличении количества опытов стремится к вероятности то и математическое ожидание совокупности можно рассчитать по формуле:
μ= ∑xi*pi .
В зависимости от характера имеющихся данных среднеарифметическое значение выборочных данных может быть рассчитано по разным формулам и в зависимости от этого она имеет разные названия. Широко используются четыре разновидности среднеарифметического значения.
1. Среднеарифметическое простое, не взвешенное значение, рассчитывается по приведенной уже формуле:
χ=∑xi/n.
Можно легко рассчитать среднеарифметическое значение данных приведенных в таблице:
| Содержание компонента в пробе (xi) | Количество проб (mi) | xi * mi |
| Всего - 8 | Всего - 1720 |
χ = 1720/8 = 215.
2. Среднеарифметическое значение - взвешенное, рассчитывается по формуле:
χ=(x1*L1+x2*L2+x3*L3+…..xi*Li)/(L1+L2+L3…+ Ln) = ∑xi*Li/∑Li, где L – длина пробы.
Среднеарифметическое взвешенное значение возникает в геологической практике, когда берутся пробы, в которых производят измерения компонентов, разной длины. В этом случае подсчет среднего значения без взвешивания на длину пробы, приведет к ошибочному результату, так как не будет сохраняться пропорциональность, поэтому используют для расчета формулу взвешенного значения. Можно рассчитать средневзвешенное значение компонента из данных, приведенных в таблице по формуле.
| L – длина пробы | Xi – значение компонента в % |
| 0.2 | |
| 2.5 | 0.5 |
| 1.8 | 0.3 |
χ= (2*0.2+2.5*0.5+1.8*0.3)/(2+2.5+1.8)=0.347
Однако для учета пропорциональности используется и другой подход, часто средние значения и другие статистики рассчитывают после приведения длин проб к одной длине и пересчета содержаний компонентов на эту длину. Этот способ получил название – композитирования (compositing) проб, а такие пробы называют композитными пробами, в этом случае можно говорить о средневзвешенных значениях проб с учетом предварительного композитирования или о средневзвешенном композитном значении изучаемой переменной. В этом случае, если мы хотим композитировать на среднюю длину пробы в 2 метра, то нужно будет пересчитать содержания полезного компонента, как в примере, показанном в ниже располагающейся таблице.
| 0.2 | |
| 0.5 | |
| (0.5*0.5+1.5*0.3)/2 = 0.35 |
3. Средняя гармоническая взвешенная величина.
4. Средняя геометрическая величина.
Среднее гармоническое – n/1/x1+1/x2+1/x3
Средняя геометрическая величина рассчитывается по формуле:
χG = n 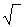 x1*x2*x3....xn = n
x1*x2*x3....xn = n 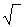 Пxi.
Пxi.
И в случае если рассчитывается средняя геометрическая взвешенная величина, то ее рассчитывают по следующей формуле:
χG = ∑m 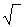 x1m1*x2m2*x3m3....xnmn = ∑m
x1m1*x2m2*x3m3....xnmn = ∑m 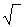 П(xi)mi,
П(xi)mi,
где mi – вес i-го варианта.
Практическое значение средних геометрических величин станет ясным при рассмотрении асимметричных распределений.
Дата добавления: 2019-04-03; просмотров: 510;
