Взаимное расположение прямой и плоскости в пространстве
Пусть в пространстве заданы плоскость 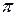 и прямая
и прямая 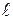 . Они могут быть 1) параллельны;
. Они могут быть 1) параллельны;
2) прямая может лежать в плоскости;
3) прямая и плоскость могут пересекаться в одной точке.
Выясним, как зная уравнения плоскости и прямой, определить их взаимное расположение.
Пусть 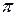 :
: 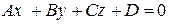 и
и 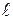 :
: 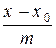
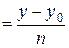
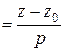 .
.
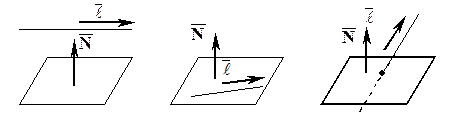
Тогда 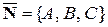 – нормальный вектор плоскости,
– нормальный вектор плоскости,
 |
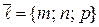 – направляющий вектор прямой.
– направляющий вектор прямой.
Если плоскость и прямая параллельны или прямая 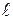 целиком лежит в плоскости
целиком лежит в плоскости 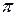 , то векторы
, то векторы 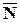 и
и 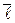 – перпендикулярны. Следовательно
– перпендикулярны. Следовательно 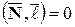 , (10)
, (10)
или в координатной форме
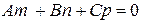 . (11)
. (11)
Если условие (10) (условие (11)) не выполняется, то геометрически это означает, что прямая и плоскость пересекаются в одной точке.
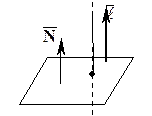 Частным случаем пересечения прямой и плоскости в одной точке является перпендикулярность прямой и плоскости. В этом случае
Частным случаем пересечения прямой и плоскости в одной точке является перпендикулярность прямой и плоскости. В этом случае 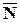 и
и 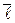 будут параллельны, что аналитически означает справедливость равенства
будут параллельны, что аналитически означает справедливость равенства
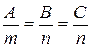 .
.
Теперь укажем условие, которое позволит различать случай параллельности прямой и плоскости и случай, когда прямая принадлежит плоскости. Пусть прямая 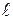 лежит в плоскости
лежит в плоскости 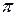 . Тогда любая точка прямой лежит в плоскости и, следовательно, ее координаты удовлетворяют уравнению плоскости. В частности,
. Тогда любая точка прямой лежит в плоскости и, следовательно, ее координаты удовлетворяют уравнению плоскости. В частности,
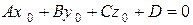 ,
,
где 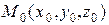 – некоторая фиксированная точка прямой
– некоторая фиксированная точка прямой 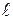 . Если же прямая параллельна плоскости, то она не имеет общих точек с плоскостью и, следовательно, для такой прямой
. Если же прямая параллельна плоскости, то она не имеет общих точек с плоскостью и, следовательно, для такой прямой
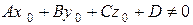 .
.
Таким образом, если прямая лежит в плоскости, то должны выполняться два условия:
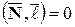 и
и 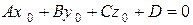 ;
;
если же прямая параллельна плоскости, то
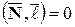 , но
, но 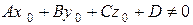 ,
,
где 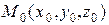 – некоторая фиксированная точка прямой
– некоторая фиксированная точка прямой 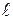 .
.
В заключение этого пункта вернемся к случаю, когда прямая и плоскость пересекаются в одной точке, и получим формулу для нахождения угла между прямой и плоскостью.
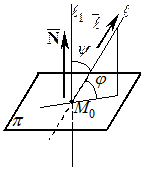 ОПРЕДЕЛЕНИЕ. Углом между прямой
ОПРЕДЕЛЕНИЕ. Углом между прямой 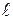 и плоскостью
и плоскостью 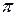 называется угол
называется угол 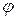 между прямой
между прямой 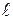 и ее проекцией на плоскость
и ее проекцией на плоскость 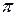 .
.
Из определения следует, что угол между прямой и плоскостью не превышает 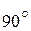 , т.е. угол острый.
, т.е. угол острый.
Пусть 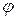 – угол между прямой
– угол между прямой 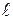 и плоскостью
и плоскостью 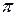 ,
, 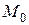 – их точка пересечения.
– их точка пересечения.
Через 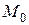 перпендикулярно плоскости
перпендикулярно плоскости 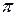 проведем прямую
проведем прямую 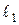 . Для
. Для 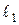 вектор
вектор 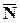 является направляющим и, следовательно, острый угол
является направляющим и, следовательно, острый угол 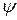 между прямыми
между прямыми 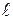 и
и 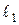 может быть найден по формуле
может быть найден по формуле
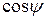
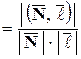 .
.
Но 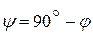 ,
,
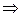
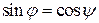
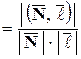 – формула для определения угла между прямой
– формула для определения угла между прямой 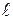 и плоскостью
и плоскостью 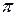 .
.
Дата добавления: 2018-11-25; просмотров: 1150;
