Отрицательное биноминальное и геометрическое распределения случайной величины.

Другие практические задачи могут быть сформулированы иначе, чем предыдущая задача относительно расчета вероятности успеха при ограниченном количестве ресурсов. Предположим, что некоторая корпорация собирается открыть два новых скрытых рудных тела на флангах известного давно эксплуатируемого месторождения, причем чтобы достичь этой цели специалисты корпорации собираются пробурить столько скважин, сколько потребуется. Можно исследовать вероятность того, что для того, чтобы достичь цели потребуется 2, 3, 4 …..n разведочных скважин до того как будут пробурены две последние продуктивные разведочные скважины. Практически в этом случае почти те же особенности, что и в предыдущей задачи, для решения которой использовалась формула биноминального распределения, то есть:

1) имеется только два исхода – успех и неудача,

2) исход каждого испытания не зависит от предыдущих исходов и вероятность успеха не меняется от испытания к испытанию,

3) но вместо условия “испытания повторяются фиксированное число раз”, здесь мы имеем дело с новым условием – “испытания продолжаются столько, сколько потребуется для достижения цели”.

Вероятностное распределение, удовлетворяющее условиям данного эксперимента, называется отрицательным биноминальным распределением. В этом случае n – число испытаний не задано. Можно рассчитать вероятность того, что будет пробурено x пустых скважин, раньше, чем будет сделано r открытий. Отрицательное биноминальное распределение можно записать в виде следующей формулы

P(r) = [(r+x-1)!/((r-1)!* x!)] * (1-p)^x * p^r.

Эта формула хорошо корреспондирует с формулой биноминального распределения, здесь выражение r+x-1 – означает, что последняя из последовательно буримых скважин, должна быть r успехом и соответствует общему количеству скважин n, а x соответствует n-r и r соответствует (r-1) в формуле биноминального распределения. Предполагая, что вероятность обнаружения промышленных залежей в данном районе равна 10% (p = 0.1), можно вычислить вероятность того, что программа поисково-разведочных работ, включающая две скважины будет успешной и эти две скважины вскроют рудные залежи, эта вероятность равна

P(r)= [(2+0-1)!/(2-1)!*0!] * [(1-0.1)⁰ * 0.1²] = 0.01.

Вероятность того, что для достижения успеха в двух испытаниях требуется пять скважин равна

P(r)= [(2+3-1)!/(2-1)!*3!] * [(1-0.1)³ * 0.1²] = 0.029.

Ясно, что вычисленные вероятности низки и поэтому можно рассчитать вероятность того, что более x скважин должно быть пробурено до того, как цель будет достигнута. Если построить график распределения в кумулятивной форме, а потом перевернуть график, то есть вычесть из 1 оценки вероятности успехов геологоразведочных программ с разным постоянно увеличивающемся количеством скважин, то получим график отрицательного распределения. Анализ этого графика показывает, что в данном случае почти на сто процентов нужно пробурить более 2 и больше скважин, чтобы достичь успеха в конкретной задаче.

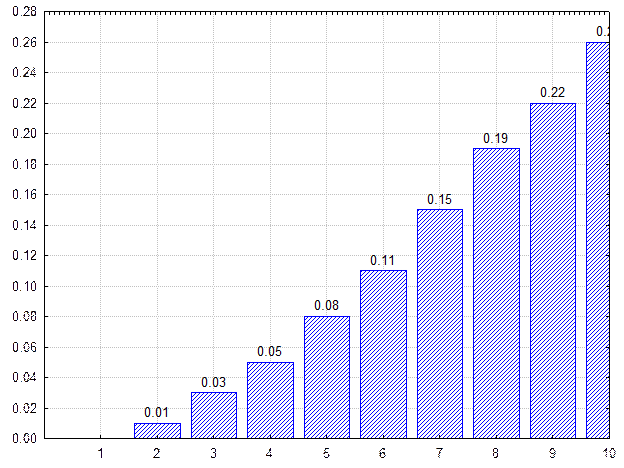
Рис. Дискретное распределение, показывающее вероятность того, что две скважины из увеличивающего их количества окажутся продуктивными при общей вероятности обнаружения залежей в данном районе в 10%.

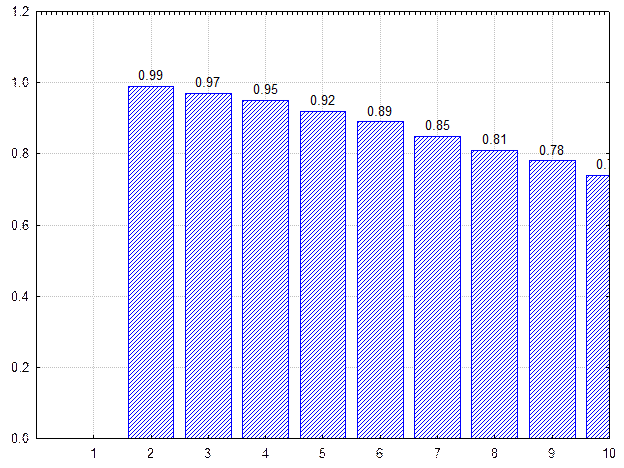
Рис. Дискретное распределение, показывающее вероятность того, что нужно пробурить скважин больше заданного, чтобы получить 2 продуктивные скважины при общей вероятности обнаружения залежей в данном районе в 10%.

Геометрическое распределение является частным случаем отрицательного биноминального распределения и используется в тех случаях, когда интерес направлен на число испытаний, предшествующих первому успеху.