Аксиоматическое определение вероятности
Аксиоматическое построение теории вероятностей создано в начале 30-х годов А.Н. Колмогоровым. Аксиомы теории вероятностей вводятся таким образом, чтобы вероятность события обладала основными свойствами статистической вероятности, характеризующей ее практический смысл. В этом случае теория хорошо согласуется с практикой.
Пусть Ω - множество всех возможных исходов некоторого опыта (эксперимента), S - алгебра событий. Напомним, что совокупность S подмножеств множества Ω, называется алгеброй (σ-алгеброй), если выполнены следующие условия:
1. S содержит невозможное и достоверное события.
2. Если события 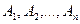 (конечное или счетное множество) принадлежат S, то S принадлежит сумма, произведение и дополнение (т. е. противоположное для
(конечное или счетное множество) принадлежат S, то S принадлежит сумма, произведение и дополнение (т. е. противоположное для 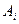 ) этих событий.
) этих событий.
Вероятностью называется функция Р(А), определенная на алгебре событий S, принимающая действительные значения и удовлетворяющая следующим аксиомам:
А1. Аксиома неотрицательности: вероятность любого события 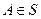 неотрицательна, т.е.
неотрицательна, т.е.
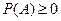 .
.
А2. Аксиома нормированности: вероятность достоверного события равна единице, т.е.
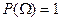 .
.
A3. Аксиома аддитивности: вероятность суммы несовместных событий равна сумме вероятностей этих событий, т. е. если 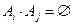
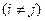 , то
, то
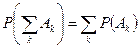 .
.
Совокупность объектов (Ω, S, Р), где Ω - пространство элементарных событий, S - алгебра событий, Р - числовая функция, удовлетворяющая аксиомам А1-АЗ, называется вероятностным пространством случайного эксперимента.
Вероятностное пространство служит математической моделью любого случайного явления; заданием этого пространства завершается аксиоматика теории вероятностей.
Свойства вероятностей
Приведем ряд свойств вероятности, являющихся следствием аксиом Колмогорова.
С1. Вероятность невозможного события равна нулю, т.е.
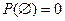 .
.
С2. Сумма вероятностей противоположных событий равна единице, т.е.
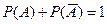 .
.
СЗ. Вероятность любого события не превосходит единицы, т.е.
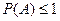 .
.
С4. Если 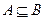 , т.е. событие А влечет за собой событие В,то
, т.е. событие А влечет за собой событие В,то
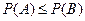 .
.
С5. Если события 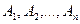 образуют полную группу несовместных событий, т.е.
образуют полную группу несовместных событий, т.е. 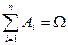 и
и 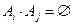 , то
, то 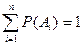 .
.
Дата добавления: 2017-03-29; просмотров: 977;
