Предмет теории вероятностей

Любая точная наука изучает не сами явления, протекающие в природе, в обществе, а их математические модели, т.е. описание явлений при помощи набора строго определенных символов и операций над ними. При этом для построения математической модели реального явления во многих случаях достаточно учитывать только основные факторы, закономерности, которые позволяют предвидеть результат опыта (наблюдения, эксперимента) по его заданным начальным условиям. Этим и занимаются большинство математических дисциплин. Обнаруженные закономерности явления называются детерминистическими(определенными).

Существует множество задач, для решения которых приходится учитывать и случайные факторы, придающие исходу опыта элемент неопределенности. Например, в вопросах стрельбы по цели невозможно без учета случайных факторов ответить на вопрос: сколько ракет нужно потратить для поражения цели? Невозможно предсказать, какая сторона выпадет при бросании монеты. Сколько лет проживет родившийся сегодня ребенок? Сколько времени проработает купленный нами телевизор? Сколько студентов опоздают на лекцию по теории вероятностей? Такие задачи, исход которых нельзя предсказать с полной уверенностью, требуют изучения не только основных, главных закономерностей, определяющих явление в общих чертах, но и случайных, второстепенных факторов. Выявленные в таких задачах (опытах) закономерности называются статистическими (или вероятностными).Статистические закономерности исследуются методами специальных математических дисциплин - теории вероятностей и математической статистики.

Теория вероятностей - математическая наука, изучающая закономерности, присущие массовым случайным явлениям. При этом изучаемые явления рассматриваются в абстрактной форме независимо от их конкретной природы. То есть теория вероятностей рассматривает не сами реальные явления, а их упрощенные схемы - математические модели.

Предметом теории вероятностейявляются математические модели случайных явлений. При этом под случайным явлениемпонимают явление, предсказать исход которого невозможно, т.к. при неоднократном воспроизведении одного и того же опыта оно протекает каждый раз несколько по-иному. Примеры случайных явлений:выпадение герба при подбрасывании монеты, выигрыш по купленному лотерейному билету, результат измерения какой- либо величины, длительность работы телевизора и т.п.

Цель теории вероятностей- осуществление прогноза в области случайных явлений, влияние на ход этих явлений, контроль их, ограничение сферы действия случайности. В настоящее время нет практически ни одной области науки, в которой в той или иной степени не применялись бы вероятностные методы.

Случайные события, их классификация

Сначала определим понятие «случайное событие» исходя из его интуитивного, наглядного понимания. Пусть проводится некоторый опыт (эксперимент, наблюдение, испытание), исход которого предсказать заранее нельзя. Такие эксперименты в теории вероятностей называют случайными. При этом рассматриваются только такие эксперименты, которые можно повторять, хотя бы теоретически, при неизменном комплексе условий произвольное число раз.

Случайным событием(или просто: событием)называется любой исход опыта, который может произойти или не произойти.

События обозначаются, как правило, заглавными буквами латинского алфавита: А, В, С, D, ... .

Пример 1.1.Опыт: бросание игральной кости; событие А - выпадение 5 очков, событие В - выпадение четного числа очков, событие С - выпадение 7 очков, событие D - выпадение целого числа очков, событие Е - выпадение не менее 3-х очков, ....

Непосредственные исходы опыта называются элементарными событиями и обозначаются через w. Элементарные события рассматриваются как неразложимые и взаимоисключающие исходы 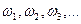этого опыта.

Множество всех элементарных событий называется пространством элементарных событий или пространством исходов и обозначается через Ω.

В примере 1.1. 6 элементарных событий 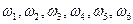_. Событие 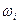означает, что в результате бросания кости выпало i очков, 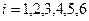. Пространство элементарных событий таково, что 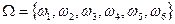или .

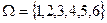Событие называется достоверным, если оно обязательно наступит в результате данного опыта, обозначается через Ω .

Событие называетсяневозможным,если оно заведомо не произойдет в результате проведения опыта, обозначается через .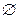

В примере 1.1 события А и В - случайные, событие С - невозможное, событие D - достоверное.

Два события называются несовместными, если появление одного из них исключает появление другого события в одном и том же опыте, т. е. не смогут произойти вместе в одном опыте. В противном случае события называются совместными.

Так, в примере 1.1 события А и В - несовместные, А и Е - совместные.

События 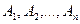называются попарно-несовместными, еслилюбые два из них несовместны.

Несколько событий образуют полную группу, еслиони попарно несовместны и в результате каждого опыта происходит одно и только одно из них.

В примере 1.1 события 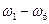образуют полную группу, 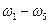- нет.

Несколько событий в данном опыте называются равновозможными,если ни одно из них не является объективно более возможным, чем другие, т.е. все события имеют равные «шансы».

В примере 1.1 элементарные события 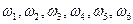равновозможные. Выпадение герба (А) или цифры (В)при бросании монеты - равновозможные события, если, конечно, монета имеет симметричную форму, не погнута, ....

Действия над событиями

Введем основные операции над событиями; они полностью соответствуют основным операциям над множествами.

Суммой событийА и В называется событие 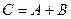,состоящее в наступлении хотя бы одного из них (т.е. или А, или В, или А и В вместе).

Произведением событийА и В называется событие 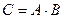,состоящее в совместном наступлении этих событий (т.е. и А и Водновременно).

Разностью событийА и В называется событие 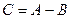,происходящее тогда и только тогда, когда происходит событие А,но не происходит событие В.

Противоположным событиюА называется событие 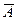,которое происходит тогда и только тогда, когда не происходит событие А (т.е. 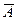означает, что событие А не наступило).

Событие А влечет событие В (или А является частным случаем В), если из того, что происходит событие А, следует, что происходит событие В: записывают .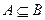

Есл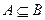и и 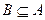, то события А и В называются равными: записывают .

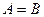Так, в примере 1.1 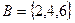, , 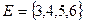, 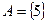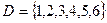. Тогда: , , , , , .

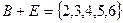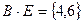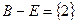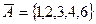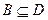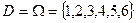События и действия над ними можно наглядно иллюстрировать с помощью диаграмм Эйлера-Венна:достоверное событие Ω изображается прямоугольником; элементарные случайные события - точками прямоугольника; случайное событие - областью внутри него.

Действия над событиями можно изобразить так, как показано на рис. 1-5.

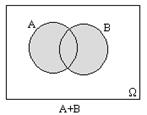
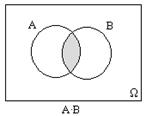
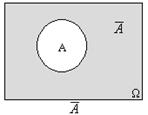
Рис 1. Рис 2. Рис 3.

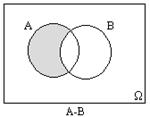
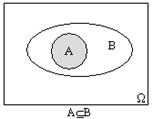
Рис. 4 Рис. 5

Операции над событиями обладают следующими свойствами:

1. 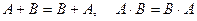(переместительное).

2. 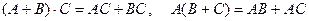(распределительное).

3. 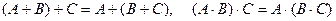(сочетательное).

4.

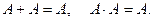
5.

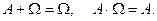
6.

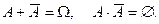
7.

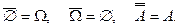
8. .

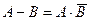9. 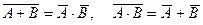(законы де Моргана)

В их справедливости можно убедиться с помощью диаграмм Эйлера-Венна.

Случайные события. Алгебра событий. (Теоретико-множественная трактовка)

Определим теперь основные понятия теории вероятностей, следуя теоретико-множественному подходу, разработанному А.Н. Колмогоровым А. Н. в 1933 году.

Пусть производится некоторый опыт со случайным исходом. Множество 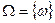всех возможных взаимоисключающих исходов данного опыта называется пространством элементарных событий (коротко ПЭС), а сами исходы- элементарными событиями(или элементами, точками).

Случайным событиемА(или просто событием А)называется любое подмножество множества Ω, если Ωконечно или счетно (т.е. элементы этого множества можно пронумеровать с помощью множества натуральных чисел): .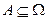

Элементарные события, входящие в подмножество А пространства Ω, называются благоприятствующими событию А.

Множество Ω, называется достовернымсобытием. Ему благоприятствует любое элементарное событие; в результате опыта оно обязательно произойдет.

Пустое множество 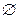называется невозможнымсобытием, т.е. в результате опыта оно произойти не может.

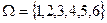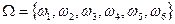Пример 1.2.Опыт: Один раз бросают игральную кость. В этом случае ПЭС таково: или ,где 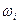- элементарное событие, состоящее в выпадении грани с i точками 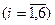. В данном случае Ω,конечно. Примером события А является, например, выпадение нечетного числа очков; очевидно, что 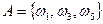; событию А благоприятствуют элементарные события 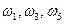. Однако если нас интересует только факт выпадения четного числа очков, то ПЭС можно построить инач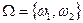е , где 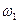- выпадение четного числа очков, 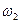- нечетного.

Над событиями можно проводить все операции, выполнимые для множеств.

Сумма(или объединение) двух событий АÎΩи ВÎΩ (обозначается А+В или AÈВ)- это множество, которое содержит элементы, принадлежащие хотя бы одному из событий А и В.

Произведениедвух событий АÎΩи ВÎΩ (обозначается АВ или АÇВ)- это множество, которое содержит элементы, общие для событий А и В.

Разность событий АÎΩи ВÎΩ (обозначается А - В или А\В ) - это множество, которое содержит элементы события А, не принадлежащие событию В.

Противоположное событию АÎΩсобытие 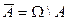. ( 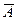называют также дополнением множества А).

СобытиеАвлечет событие В (обозначается 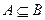), если каждый элемент события А содержится в В.

По определению: 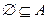для любого А.

События А и В называются несовместными, если их произведение есть невозможное событие, т.е. .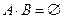

Несколько событий 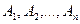образуют полную группу несовместных событий, если их сумма представляет все ПЭС, а сами события несовместны, т.е. 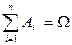и 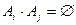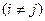. Полную группу образуют, например, события А и ( , ).

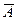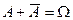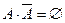В случае несчетного пространства Ω в качестве событий рассматриваются не все подмножества Ω, а лишь некоторые классы этих подмножеств, называемые алгебрами и σ-алгебрами множеств.

Класс S подмножеств пространства Ω называется алгеброй множеств (событий), если:

1. , ;

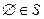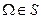2. из 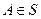вытекает, что ;

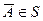3. из 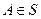, 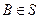вытекает, что , .

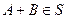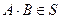Заметим, что в условии 3 достаточно требовать либо 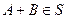, либо 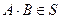, так как , .

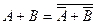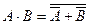Алгебру событий образует, например, система подмножеств 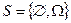. Действительно, в результате применения любой из вышеприведенных операций к любым двум элементам класса S снова получается элемент данного класса: , , , .

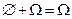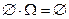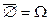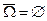При расширении операций сложения и умножения на случай счетного множества алгебра множеств S называется σ-алгеброй, если из 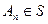, 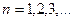следует 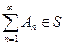, 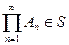(достаточно требовать либо 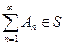, либо ).

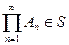Множество всех подмножеств множества Ω, если оно конечно или счетно, образует алгебру.