Свойство статистической устойчивости относительной частоты события
Пусть в n повторяющихся опытах некоторое событие А наступило 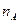 раз.
раз.
Число 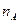 называется частотой, события А, а отношение:
называется частотой, события А, а отношение:
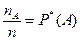
| (1.1) |
называется относительной частотой (или частостью)события А в рассматриваемой серии опытов.
Относительная частота события обладает следующими свойствами:
1. Частость любого события заключена между нулем и единицей, т.е.
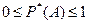 .
.
2. Частость невозможного события равна нулю, т.е.
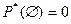
3. Частость достоверного события равна 1, т.е.
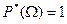 .
.
4. Частость суммы двух несовместных событий равна сумме частоты
этих событий, т.е. если 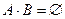 , то
, то
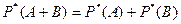 .
.
Частость обладает еще одним фундаментальным свойством, называемым свойством статистической устойчивости: с увеличением числа опытов (т.е. n) она принимает значения, близкие к некоторому постоянному числу (говорят: частость стабилизируется, приближаясь к некоторому числу, частость колеблется около некоторого числа, или ее значения группируются около некоторого числа).
Так, например, в опыте (К. Пирсон) бросание монеты – относительная частота появления герба при 12000 и 24000 бросаниях оказалась равной 0,5015 и 0,5005 соответственно, т.е. частость приближается к числу 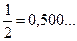 . Частость рождения мальчика, как показывают наблюдения, колеблется около числа 0,515.
. Частость рождения мальчика, как показывают наблюдения, колеблется около числа 0,515.
Отметим, что теория вероятностей изучает только те массовые случайные явления с неопределенным исходом, для которых предполагается наличие устойчивости относительной частоты.
Статистическое определение вероятности
Для математического изучения случайного события необходимо ввести какую-либо количественную оценку события. Понятно, что одни события имеют больше шансов («более вероятны») наступить, чем другие. Такой оценкой является вероятность события, т.е. число, выражающее степень возможности его появления в рассматриваемом опыте. Математических определений вероятности существует несколько, все они дополняют и обобщают друг друга.
Рассмотрим опыт, который можно повторять любое число раз (говорят: «проводятся повторные испытания»), в котором наблюдается некоторое событие А.
Статистической вероятностьюсобытия А называется число, около которого колеблется относительная частота события Апри достаточно большом числе испытаний (опытов).
Вероятность события А обозначается символом Р(А). Согласно данному определению:
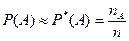 . .
| (1.2) |
Математическим обоснованием близости относительной частоты 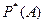 и вероятности Р(А) некоторого события А служит теорема Я. Бернулли.
и вероятности Р(А) некоторого события А служит теорема Я. Бернулли.
Вероятности Р(А) приписываются свойства 1-4 относительной частоты:
1. Статистическая вероятность любого события заключена между нулем и единицей, т.е.
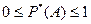 .
.
2. Статистическая вероятность невозможного события равна нулю, т.е.
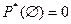 .
.
3. Статистическая вероятность достоверного события равна 1, т.е.
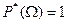 .
.
4. Статистическая вероятность суммы двух несовместных событий равна сумме частоты этих событий, т.е. если 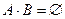 , то
, то
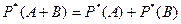 .
.
Статистический способ определения вероятности, опирающийся на реальный опыт, достаточно полно выявляет содержание этого понятия. Недостатком статистического определения является неоднозначность статистической вероятности; так в примере с бросанием монеты в качестве вероятности можно принять не только число 0,5, но и 0,49 или 0,51 и т.д. Для надежного определения вероятности нужно проделать большое число испытаний, что не всегда просто или дешево.
Классическое определение вероятности
Существует простой способ определения вероятности события, основанный на равновозможности любого из конечного числа исходов опыта. Пусть проводится опыт с n исходами, которые можно представить в виде полной группы несовместных равновозможных событий. Такие исходы называются случаями, шансами, элементарными событиями, опыт - классическим. Про такой опыт говорят, что он сводится к схеме случаев или схеме урн (т.к. вероятностную задачу для такого опыта можно заменить эквивалентной ей задачей с урнами, содержащими шары разных цветов).
Случай w, который приводит к наступлению события А, называется благоприятным(или благоприятствующим) ему, т.е. случай w влечет событие A: 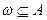 .
.
Вероятностью события А называется отношение числа m случаев, благоприятствующих этому событию, к общему числу n случаев, т.е.
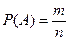 . .
| (1.3) |
Наряду с обозначением Р(А) для вероятности события А используется обозначение р, т.е. р=Р(А).
Из классического определения вероятности вытекают следующие свойства:
1. Вероятность любого события заключена между нулем и единицей, т.е.
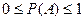 .
.
2. Вероятность невозможного события равна нулю, т.е.
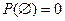 .
.
3. Вероятность достоверного события равна 1, т.е.
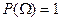 .
.
4. Вероятность суммы несовместных событий равна сумме частоты этих событий, т.е. если 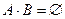 , то
, то
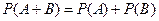 .
.
Пример 1.3. В урне находятся 12 белых и 8 черных шаров. Какова вероятность того, что наудачу вынутый шар будет белым?
Решение:
Пусть А – событие, состоящее в том, что вынут белый шар. Ясно, что 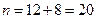 – число всех равновозможных случаев. Число случаев, благоприятствующих событию А, равно 12, т.е.
– число всех равновозможных случаев. Число случаев, благоприятствующих событию А, равно 12, т.е. 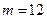 . Следовательно, по формуле (1.3) имеем:
. Следовательно, по формуле (1.3) имеем: 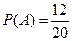 , т.е.
, т.е. 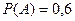 .
.
Геометрическое определение вероятностей
Геометрическое определение вероятности применяется в случае, когда исходы опыта равновозможны, а ПЭС есть бесконечное несчетное множество. Рассмотрим на плоскости некоторую область Ω, имеющую площадь 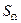 , и внутри области Ω, область D с площадью SD (см. рис. 6).
, и внутри области Ω, область D с площадью SD (см. рис. 6).
В области Ω случайно выбирается точка X. Этот выбор можно интерпретировать как бросание точки X в область Ω. При этом попадание точки в область Ω - достоверное событие, в D - случайное. Предполагается, что все точки области Ω равноправны (все элементарные события равновозможны), т.е. что брошенная точка может попасть в любую точку области Ω и вероятность попасть в область D пропорциональна площади этой области и не зависит от ее расположения и формы. Пусть событие 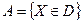 , т.е. брошенная точка попадет в область D.
, т.е. брошенная точка попадет в область D.
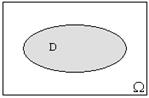
Рис. 6
Геометрической вероятностью события А называется отношение площади области D к площади области Ω, т.е.
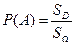 . .
| (1.4) |
Геометрическое определение вероятности события применимо и в случае, когда область Ω и D обе линейные или объемные. В первом случае:
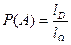 , ,
| (1.5) |
во втором:
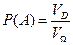 , ,
| (1.6) |
где l - длина, V – объем соответствующей области.
Все три формулы можно записать в виде:
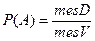 , ,
| (1.7) |
где через mes обозначена мера (S, l, V) области.
Геометрическая вероятность обладает всеми свойствами, присущими классическому определению:
1. Геометрическая вероятность любого события заключена между нулем и единицей, т.е.
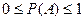 .
.
2. Геометрическая вероятность невозможного события равна нулю, т.е.
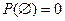 .
.
3. Геометрическая вероятность достоверного события равна 1, т.е.
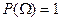 .
.
4. Геометрическая вероятность суммы несовместных событий равна сумме частоты этих событий, т.е. если 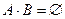 , то
, то
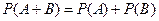 .
.
Дата добавления: 2017-03-29; просмотров: 700;
