Анализ статистической значимости коэффициента детерминации.

После оценки индивидуальной статистической значимости каждого из коэффициентов регрессии обычно анализируется совокупная значимость коэффициентов. Такой анализ осуществляется на основе проверки гипотезы об общей значимости — гипотезы об одновременном равенстве нулю всех коэффициентов регрессии при объясняющих переменных:

Я₀: β₀= β₁= β₂ = ... = β_m=0

Если данная гипотеза не отклоняется, то делается вывод о том, что совокупное влияние всех m объясняющих переменных X₁, Х₂, ..., Х_m модели на зависимую переменную Y можно считать статистически несущественным, а общее качество уравне­ния регрессии невысоким.

Проверка данной гипотезы осуществляется на основе дисперсионного анализа сравнения объясненной и остаточной дисперсий.

H₀: (объясненная дисперсия) = (остаточная дисперсия),

H₁: (объясненная дисперсия) > (остаточная дисперсия).

Строится F-статистика:

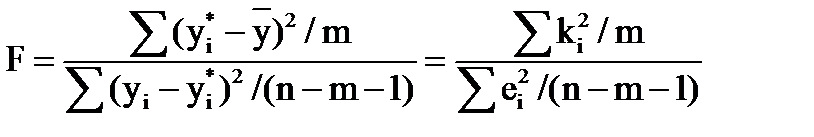
где 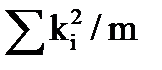— объясненная дисперсия; 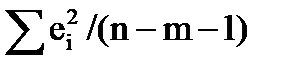— остаточная дисперсия. При выполнении предпосылок МНК построенная F-статистика имеет распределение Фишера с числами степеней свободы ν₁=m, ν₂= n-m-1. Поэтому, если при требуемом уровне значимости α F_набл > F_α,m,n-m-1= F_кр (критическая точка распределения Фишера), то H₀ отклоняется в пользу H₁. Это означает, что объясненная дисперсия существенно больше остаточной дисперсии, а следовательно, уравнение регрессии достаточно качественно отражает динамику изменения зависимой переменной Y.

Однако на практике чаще вместо указанной гипотезы проверяют тесно связанную с ней гипотезу о статистической значимости коэффициента детерминации R²:

Для проверки данной гипотезы используется следующая F-статистика:

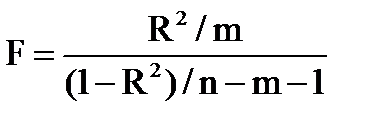
Величина F при выполнении предпосылок МНК и при справедливости. Но имеет распределение Фишера, аналогичное распределению F-статистики.

Анализ статистики F позволяет сделать вывод о том, что для принятия гипотезы об одновременном равенстве нулю всех коэффициентов линейной регрессии коэффициент детерминации R² не должен существенно отличаться от нуля. Его критическое значение уменьшается при росте числа наблюдений и может стать сколь угодно малым.