Двухфакторный дисперсионный анализ
Двухфакторный дисперсионный анализ с однократными наблюдениями на каждой комбинации уровней определяется следующей расчетной схемой (табл. 5).
Таблица 5
Расчетная схема двухфакторного дисперсионного анализа
| Источник изменчивости | Сумма квадратов отклонений | Число степеней свободы | Дисперсия | F-критерий |
| Фактор А (k уровней) | 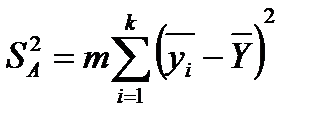
| k-1 | 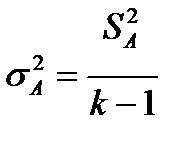
| 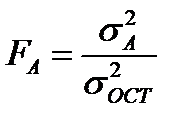
|
| Фактор B (m уровней) | 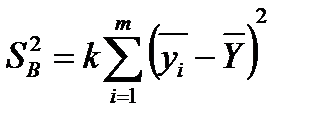
| m-1 | 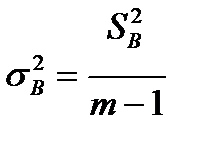
| 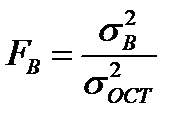
|
| Случайная составляющая | 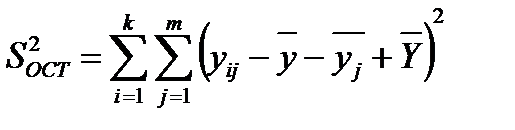
| (k-1)(m-1) | 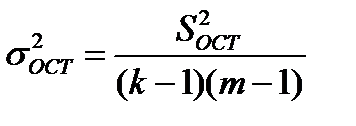
|
Пример. Четыре различных типа покрышек испытывались на автомобилях четырех различных марок. Измерялся износ шин в мм после пробега 40 тысяч км.
Получены следующие результаты:
| Тип покрышек | Марка автомобиля (фактор В на 4 уровнях) | |||
| ВОЛГА | ЖИГУЛИ | ШКОДА | МОСКВИЧ | |
Влияет ли тип покрышек и марка автомобиля на износ шин?
Решение. Имеем задачу двухфакторного дисперсионного анализа с однократным наблюдением на каждой комбинации уровней (к=4,m = 4). Следовательно, можно воспользоваться схемой расчета, приведенной в табл. 4.
По имеющимся исходным данным получаем:
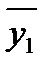 =11;
=11; 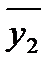 =9.75;
=9.75; 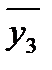 =8.75;
=8.75; 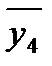 =6.75;
=6.75;
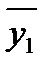 = 11,25;
= 11,25; 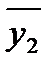 = 9.25;
= 9.25; 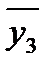 = 7.75;
= 7.75; 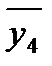 = 8.00;
= 8.00;
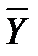 =9.06.
=9.06.
Другие результаты вычислений представлены в табл. 5
Таблица 5
Результаты расчета примера двухфакторного дисперсионного анализа
| Источник изменчивости | Сумма квадратов отклонений | Число степеней свободы | Дисперсия | FH |
| Фактор А | 30.6 | 10.2 | 7.8 | |
| Фактор В | 38.6 | 12.9 | 9.9 | |
| Случайная составляющая | 11.7 | 1.3 | ||
| Общая изменчивость | 80.9 |
Критические значения критерия находим по таблицам квантилей F-распределения:
Fkp = F(0.99; 3; 9) = 7.0; Fkp = F(0.95; 3; 9) = 3.86.
Так как FH > Fkp для фактора А и для фактора В, то гипотеза Н0 – о равенстве износов на каждом уровне отвергается, и принимается конкурирующая гипотеза H1 - средние износы на различных уровнях различны.
Следовательно, различные типы покрышек и марки автомобилей влияют на износ покрышек (шин). Поэтому не безразлично, какие покрышки устанавливаются на автомобили той или иной марки.
Вопросы для повторения
1. В чем разница между корреляционной и функциональной связями?
2. Какие основные проблемы и каким образом решает исследователь при изучении корреляционных зависимостей?
3. Для чего рассчитываются частные коэффициенты корреляции?
4. Как проверяются гипотезы в корреляционном анализе?
5. Какие показатели являются мерой тесноты связи между количественными признаками?
6. Как оценить существенность линейного коэффициента корреляции?
7. Какие показатели используют для измерения тесноты связи между качественными признаками?
8. В чем состоит смысл индекса корреляции и коэффициента множественной корреляции?
9. Что характеризует коэффициент детерминации?
10. Какая существует связь между линейным коэффициентом корреляции и коэффициентом регрессии?
11. Какое значение имеет расчет индекса корреляции?
12. Поясните отличие коэффициента корреляции от корреляционного отношения.
13. Какая гипотеза проверяется в дисперсионном анализе?
Резюме по теме
Основной задачей корреляционного анализа является измерение тесноты связи между переменными (случайными величинами) путем точечной и интервальной оценок соответствующих коэффициентов (характеристик).
С помощью корреляционного анализа производиться отбор факторов, оказывающих наиболее существенное влияние на результативный признак (на основании степени связи между ними), обнаружение ранее неизвестных причинных связей.
Корреляция непосредственно не выявляет причинных связей между переменными, но устанавливает численное значение тесноты этих связей и достоверность суждений об их наличии.
Дата добавления: 2017-09-19; просмотров: 341;
