Расчет коэффициентов в множественной линейной регрессии.

Представим данные наблюдений и соответствующие коэффициенты в матричной форме.

Y=(y₁,y₂,…y_n)^т B=(b₀,b₁,…b_m)^т e=(e₁,e₂…e_n)^т

Решение системы уравнений в матричном виде, будет иметь следующий вид:

В = (X^тX)^­-1X^тY.

Здесь (X^тX)^­-1— матрица, обратная к X^тX.

Полученные общие соотношения справедливы для уравнений регрессии с произвольным количеством m объясняющих переменных.

Пример.

Имеются следующие данные (условные) о сменной добыче угля на одного рабочего Y(т), мощности пласта X₁(м) и уровне механизации работ X₂(%), характеризующие процесс добычи угля в 10 шахтах.

Таблица 1

Предполагая, что между переменными Y, X₁,X₂ существует линейная корреляционная зависимость, найти ее уравнение регрессии.

Решение. Обозначим Y=(5,10,10,….8)^Т,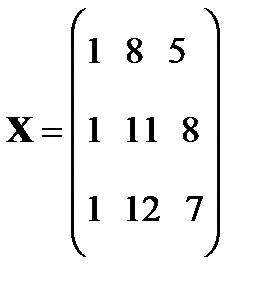

Теперь X^тX=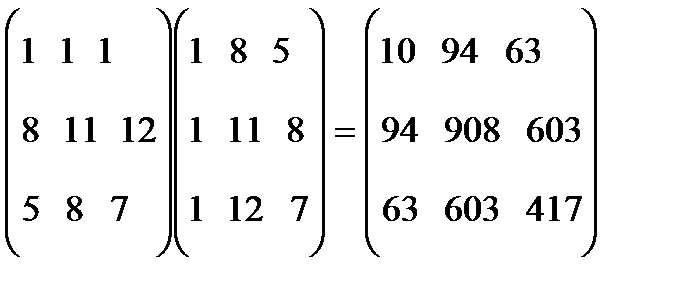

X^тY=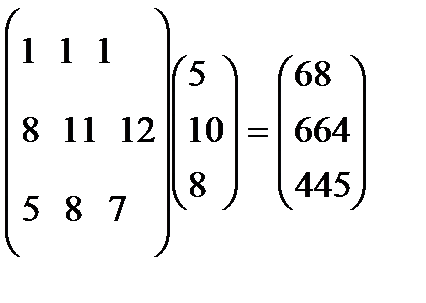

Матрицу A^-1=(X'X)^-l определим по формуле A^-1=(A*)^т /|A|

Получим

,

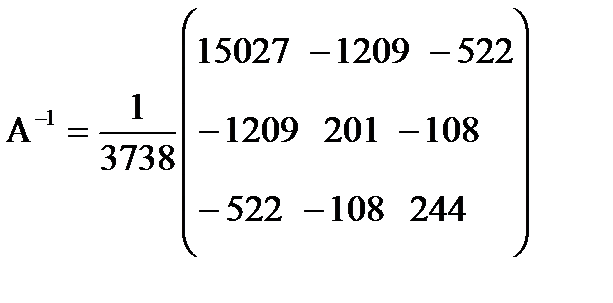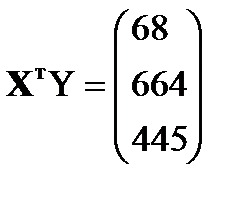
Окончательно получаем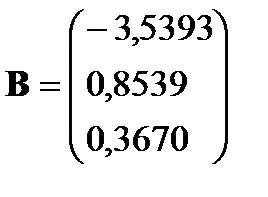

Уравнение множественной регрессии имеет вид: у=—3,54+0,854x₁+0,367x₂. Оно показывает, что при увеличении только мощности пласта Х₁ (при неизменном Х₂) на 1 м добыча угля на одного рабочего Y увеличивается в среднем на 0,854 т, а при увеличении только уровня механизации работ Х₂ (при неизменной Х₁) — в среднем на 0,367 т.

3. Дисперсии и стандартные ошибки коэффициентов.

Наиболее удобно формулы расчета данных характеристик приводить в матричной форме.

Как показано выше, эмпирические коэффициенты множественной линейной регрессии определяются по формуле:

В = (Х^Т X)^-1X^TY.

Подставляя теоретические значения Y = Хb+e в данное соотношение, имеем:

В=(Х^Т X)^-1X^T(Хb+e)=(Х^Т X)^-1X^TХb+(Х^Т X)^-1X^TХe=b+(Х^Т X)^-1X^TХe.

имеем: В-b=(Х^Т X)^-1X^TХe - вектор отклонений

Построим дисперсионно-ковариационную матрицу

D(e_i)=K(b)=M((В-b)(В-b)^т)=M((Х^Т X)^-1X^TХe((Х^Т X)^-1X^TХe)^Т)=М((Х^Т X)^-1X^Tee^ТX((Х^Т X)^-1)^Т)

В силу того что X_ij, не являются случайными величинами, имеем:

K(β)=σ²((X^TX)^-1)^TÞD(e_i)=σ²z_jj

где z_jj– диагональный элемент матрицы Z^-1=(Х^Т X)^-1.

Поскольку истинное значение дисперсии s² по выборке определить невозможно, оно заменяется соответствующей несмещенной оценкой

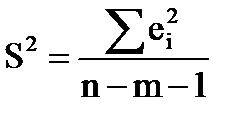
где n– число степеней свободы, m — количество объясняющих переменных модели (m-1=k – число коэффициентов β_j) .

Следовательно, по выборке мы можем определить лишь выборочные дисперсии эмпирических коэффициентов ре­грессии:

S_bj²=S²z_jj

S называется стандартной ошибкой регрессии. S_bj – называется стандартной ошибкой коэффициента регрессии.