Однофакторный дисперсионный анализ.
В дисперсионном анализе исследуется влияние одного или нескольких качественных показателей на количественный показатель.
В однофакторном дисперсионном анализе на одну количественную переменную Y оказывает влияние один фактор (один качественный показатель), наблюдаемый на k уровнях, то есть имеем k выборок для переменной Y.
Наблюдаемые данные обозначим yij, где i - индекс уровня (i = 1,2,...,k), j - индекс наблюдения на i-м уровне ( j = 1,...,ni).
На каждом уровне может быть свое число наблюдений ni.
Общее число опытов (наблюдений)
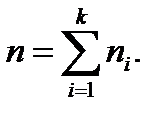
По данным yij определяются следующие характеристики:
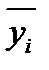- среднее значение переменной Y на i -м уровне
;
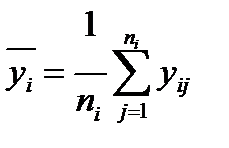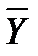- среднее значение переменной Y по всем значениям
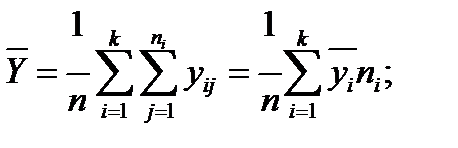
S2 - сумму квадратов отклонений наблюдений от общего среднего
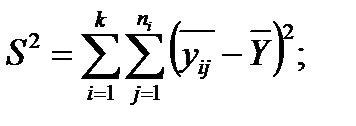
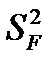- сумму квадратов отклонений средних групповых значений от общего среднего значения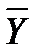 
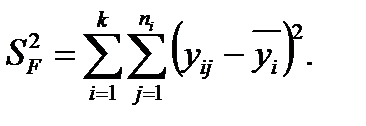
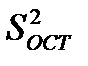- остаточную сумму квадратов отклонений
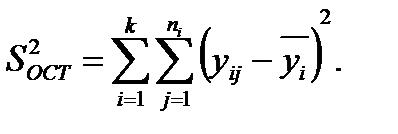
Справедливо соотношение: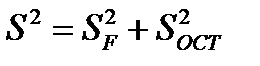 
Соответствующие суммы квадратов отклонений, отнесенные к числу степеней свободы, представляют собой несмещенные оценки соответствующих дисперсий.
Далее выполняются следующие действия:
вычисление общей дисперсии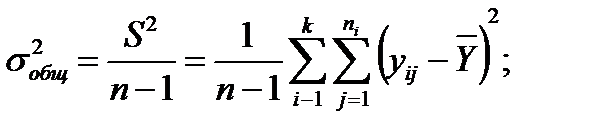 
вычисление факторной дисперсии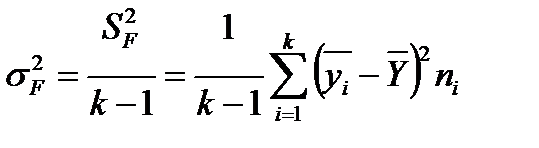 
;
вычисление остаточной дисперсии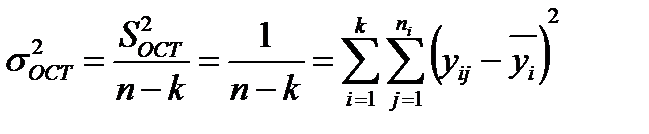 
.
В дисперсионном анализе проверяется гипотеза Н0 о равенстве средних групповых значений количественного показателя:
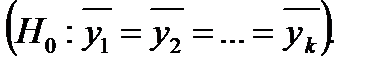
Критерием для проверки этой гипотезы является соотношение факторной дисперсии иостаточной дисперсии:
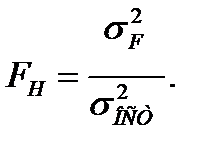
Пример.Исследовалось влияние индивидуальных качеств (особенностей, заслуг) продавцов на объемы выручки магазина. Получены следующие данные:
| Номера продавцов | Число отработанных дней | Дневная выручка магазина (тыс. долл.) |
| 16.5; 15.0; 16.2; 18.9; 20.1; 19.3; 10.1; 12.8 | ||
| 16.7; 16.3; 14.0; 15.0; 16.7; 12.4; 7.9; 9.8; 14.4; 10.8; 11.1;13.0; 10.7 | ||
| 10.7; 9.0; 13.9; 11.3; 9.4; 11.9; 10.5; 9.7; 7.4 |
Определить, влияют ли индивидуальные качества продавцов на объемы выручки магазина?
Решение.По имеющимся данным уij определим средние значения дневной выручки (переменной Y) на каждом (из трех) i-ом уровне:
.
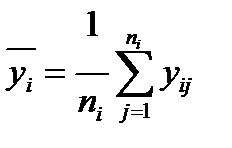Получим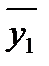 
= 16.11; 
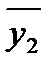= 12.98; 
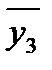= 10.44.
Среднее значение переменной Y по всем значениям
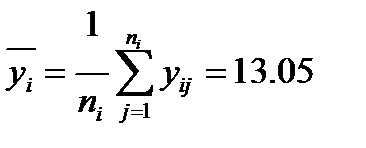
Результаты других расчетов сведены в табл.3.
Таблица 3.
Результаты расчета примера однофакторного дисперсионного анализа
| Источник изменчивости | Сумма квадратов отклонений | Число степеней свободы | Дисперсия | FH |
| Факторная (систематическая) | 131.67 | 65.83 | 8.46 | |
| Случайная составляющая | 210.05 | 7.78 | ||
| Общая изменчивость | 341.72 |
Критическое значение находим по таблицам квантилей F - распределения при уровне значимости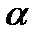 
= 0.05, что соответствует квантилю порядка 0.95.
Fkp = F(0.95; 2; 27) = 3.35.
Так как FH > Fkp , то гипотеза Н0 о равенстве дневной выручки у каждого продавца отвергается, и принимается конкурирующая гипотеза H1 - средние выручки продавцов (на различных уровнях) различны. Это означает, что индивидуальные качества (особенности) продавцов влияют на объемы выручки магазина.
Пример. Катализатор для химической реакции получался четырьмя различными способами. В экспериментах проверялась активность катализатора, причем для каждого уровня (способа получения) было сделано по пять наблюдений.
Получены следующие данные:
| Способы получения катализатора | Активность катализатора |
| А1 | 56; 55; 62; 59; 60; |
| А2 | 64; 61; 50; 55; 56; |
| А3 | 45; 46; 45; 39; 43; |
| А4 | 42; 39; 45; 43; 41; |
Необходимо проверить независимость качества (активности) катализатора от способа получения.
Решение. По имеющимся данным yij определим средние значения активности катализатора при каждом (из четырех) i-ом способе его получения.
Находим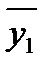 
= 58.4; 
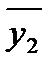= 57.2; 
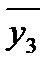= 43.6; 
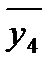= 42.0.
Среднее значение переменной Y по всем наблюдениям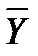 
= 50.3.
Результаты других расчетов сведены в табл. 4.2.
Таблица 4.
Результатырасчета примера однофакторного дисперсионного анализа
| Источник изменчивости | Сумма квадратов отклонений | Число степеней свободы | Дисперсия | FH |
| Факторная (систематическая) | 378.3 | 29.8 | ||
| Случайная составляющая | 203.2 | 12.7 | ||
| Общая изменчивость | 1338.2 |
Критическое значение критерия находим по таблицам квантилей F -распределения при уровне значимости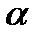 
= 0.05, что соответствует квантилю порядка 0.95:
Fkp =F(0.95;2; 27) = 3.35.
Так как FH > Fkp , то гипотеза Н0 - об одинаковой активности катализатора при различных способах его получения (на каждом уровне) отвергается, и принимается конкурирующая гипотеза Н1 - активность катализатора при различных способах его получения различна.
Дата добавления: 2017-09-19; просмотров: 196;