Дисперсионный анализ
Основной целью дисперсионного анализа является выявление на основе величины общей дисперсии влияния отдельных факторов на вариацию признака. Для оценки доли вариации, обусловленной тем или иным признаком, совокупность разделяют на группы по тому признаку, свойства которого исследуются. Это позволяет разложить общую дисперсию на 2 дисперсии, из которых одна часть вариации определяется влиянием фактора, который положен в основу группировки, а вторая – вариацией всех факторов, кроме того, который изучается. Т.е. соответственно с правилом сложения дисперсий, если данные представлены в виде аналитической группировки, определяют общую, межгрупповую, внутригрупповую дисперсии.
Общая дисперсия характеризует вариацию признака в статистической совокупности в результате влияния всех факторов.
Общая дисперсия для сгруппированных данных определяется по формуле:
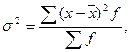
для несгруппированных даннях:
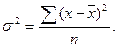
Кроме того, применяются два упрощенных способа расчета общей дисперсии:
1. Если варианты выражены небольшими числами, дисперсия определяется как разность средних:
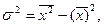
2. Если варианты выражены большими числами, то применяют способ моментов:
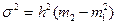 ,
,
где m1 – момент первого порядка;
m2 – момент второго порядка.
Межгрупповая дисперсия показывает уровень отклонения групповых средних от общей средней, т.е. характеризует влияние фактора, положенного в основу группировки:
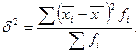
Внутригрупповая дисперсия характеризует вариацию признака в средине каждой группы статистической группировки:
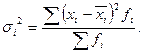
Средняя из внутригрупповых дисперсий определяется следующим образом:
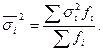
Связь между общей дисперсией, средней из групповых и межгрупповой дисперсиями можно проследить с помощью правила сложения дисперсий:
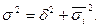
Сущность связи между признаками характеризует коэффициент детерминации, который рассчитывается как отношение межгрупповой дисперсии к общей дисперсии:
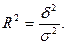
Эмпирическое корреляционное отношение – это корень квадратный из коэффициента детерминации:
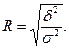
Корреляционное отношение характеризует степень приближения связи к функциональной, т.е. тесноту корреляционной зависимости и колеблется от 0 до 1.
Наряду с вариацией индивидуальных значений признака вокруг средней может наблюдаться и вариация индивидуальных долей признака вокруг средней доли.Такое изучение вариации достигается посредством вычисления и анализа следующих видов дисперсий:
- внутригрупповая: 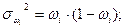
- средняя из внутригрупповых дисперсий: 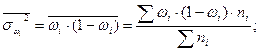
- межгрупповая: 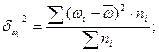
- общая: 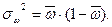
При этом 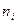 - численность единиц в отдельных группах;
- численность единиц в отдельных группах;
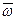 - доля изучаемого признака во всей совокупности, которая определяется по формуле:
- доля изучаемого признака во всей совокупности, которая определяется по формуле: 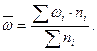
Дата добавления: 2019-04-03; просмотров: 584;
