Показатели вариации

После определения средней величины встает вопрос, в какой мере индивидуальные значения признака отличаются между собой и от средней. Для этого определяют показатели вариации.

Вариациейпризнака называют разницу в числовых значениях признаков единиц совокупности и их колебания вокруг средней величины, которая характеризует совокупность. Чем меньше вариация, тем более однородной является совокупность и более надежной (типовой) – средняя величина.

К основным абсолютным и относительным показателям, характеризующим вариацию относятся:

- размах вариации;

- среднее линейное отклонение;

- коэффициент осцилляции;

- дисперсия;

- стандартное среднее квадратическое отклонение;

- коэффициент вариации.

Размах вариации – это разница между наибольшим 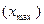и наименьшим 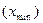значениями признака:

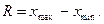
Среднее линейное отклонение – это средний модуль отклонений индивидуальных значений признака от их средней величины:

- для несгруппированных данных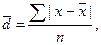

- для сгруппированных данных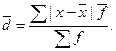

Коэффициент осциляции –это отношение размаха вариации к среднему значению признака:

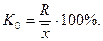
Дисперсия – это средняя арифметическая квадратов отклонений каждого значения признака от средней величины:

- для несгруппированных даннях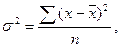

- для сгруппированных данных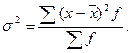

Среднее квадратическое отклонение – это обобщающая характеристика абсолютних размеров вариации признака в совокупности.Определяется как корень квадратный из дисперсии:

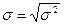
Среднее квадратическое отклонение всегда выражается в тех же единицах измерения, что и признак (в метрах, тоннах, процентах, гектарах и т.д.) и является абсолютной мерой вариации.

Чем меньше среднее квадратическое отклонение, тем более типовой является средняя и тем более однородной является совокупность.

Коэффициент вариации является относительной мерой вариации и позволяет сравнивать степень вариации признаков в рядах вариации с разным уровнем средних. Рассчитывается как отношение среднего квадратического отклонения от средней величины:

.

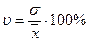Если коэффициент вариации <33 %, то такая совокупность считается однородной.