Исследование формы распределения.
Выяснение общего характера распределения предполагает не только оценку степени его однородности, но и исследование формы распределения, т.е. оценку симметричности и эксцесса.
При увеличении объема статистической совокупности (N) и одновременного уменьшения интервала группировки полигон либо гистограмма распределения все более и более приближается к некоторой плавной кривой, являющейся для указанных графиков пределом. Эта кривая называется эмпирической кривой распределения и представляет собой графическое изображение в виде непрерывной линии изменения частот, функционально связанного с изменением вариант.
В статистике различают следующие виды кривых распределения:
- одновершинные кривые (описывают однородные совокупности);
- многовершинные кривые (описывают неоднородные совокупности).
Одновершинные кривые распределения делятся на симметричные, умеренно асимметричные и крайне асимметричные.
Распределение называется симметричным, если частоты любых двух вариантов, равноотстоящих в обе стороны от центра распределения, равны между собой.
Симметричностью характеризуется нормальное распределение, для которого мода равна медиане и равна средней: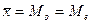 
.
Нормальный ряд распределения описывается уравнением:
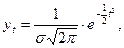
где 
- ордината кривой нормального распределения (относительная плотность распределения);
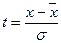- нормированное отклонение;
х – значение изучаемого признака;
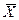– средняя арифметическая ряда;
σ – среднее квадратическое отклонение;
π = 3,1415 – математическая константа (отношение длины окружности к ее диаметру);
e = 2,7182 – основание натурального логарифма.
Следовательно, кривая нормального распределения может быть построена по двум параметрам – средней арифметической и среднему квадратическому отклонению.
Если 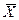не меняется, а изменяется только σ, то чем меньше σ, тем более вытянута вверх кривая и наоборот, чем больше σ, тем более плоской и растянутой вдоль оси абсцисс становится кривая нормального распределения (рис. 7.1).
|
|
|
|
|
|
|
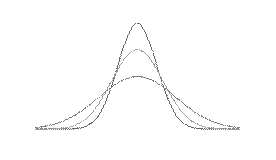
Рис. 7.1. Влияние величины σ на кривую нормального распределения
Если σ остается неизменной, а 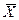изменяется, то кривые нормального распределения имеют одинаковую форму, но отличаются друг от друга положением максимальной ординаты (вершины) (рис. 7.2).
|
|
|
< 
< 
|
|
|
|
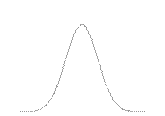
Рис. 7.2. Влияние величины 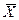на кривую нормального распределения
Итак, выделим особенности кривой нормального распределения:
1) кривая симметрична и имеет максимум в точке, соответствующей значению 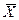=Ме=Мо;
2) кривая асимптотически приближается к оси абсцисс, продолжаясь в обе стороны до бесконечности (чем больше отдельные значения X отклоняются от 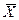, тем реже они встречаются);
3) кривая имеет две точки перегиба на расстоянии ± σ от ;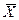
4) коэффициенты асимметрии и эксцесса равны нулю.
Коэффициенты асимметрии используют для характеристики асимметрии. Наиболее часто используется коэффициент асимметрии Пирсона:
.
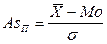В одновершинных распределениях величина этого показателя изменяется от -1 до +1.
Распределения с сильной правосторонней и левосторонней асимметрией показаны на рис. 7.3.
|
|
|
|
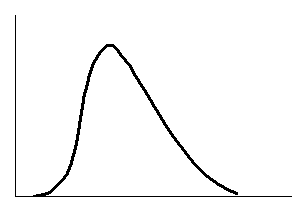
Рис. 7.3. Асимметрия распределения
Левосторонней будет такая асимметрия, когда левая часть кривой длиннее правой и вершина ее сдвинута вправо. Если вершина сдвинута влево и правая часть кривой длиннее левой, такая асимметрия называется правосторонней.
Показатель асимметрии Пирсона характеризует асимметрию в центральной части распределения, поэтому более распространенным и более точным является коэффициент асимметрии, рассчитанный на основе центрального момента 3-его порядка:
.
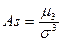Центральным моментом в статистике называется среднее отклонение индивидуальных значений признака от его среднеарифметической величины (табл.7.1).
Таблица 7.1
Центральные моменты
| Порядок момента | Формула | |
| для несгруппированных данных | для сгруппированных данных | |
| Первый μ1 |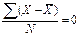 
| 
|
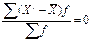
| Второй μ2 |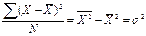 
| 
|
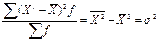
| Третий μ3 |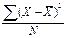 
| 
|
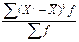
| Четвертый μ4 | 
| 
|
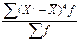
С помощью момента четвертого порядка характеризуется еще более сложное свойство рядов распределения – эксцесс(от англ. «излишество»). Показатель эксцесса рассчитывается по формуле:
.
Эксцессявляется показателем островершинности расределения. При симметричных распределениях он равен нулю, если эксцесс больше нуля, то распределение относится к островершинным, если меньше нуля – к плосковершинным (рис.7.4.).
|
|
|
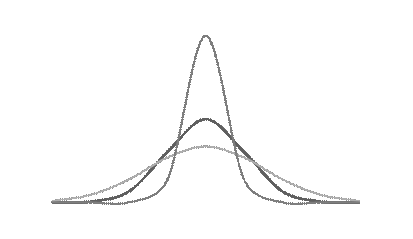
Рис. 1.4. Эксцесс распределения
По значениям показателей асимметрии и эксцесса распределения можно судить о близости распределения к нормальному: показатели асимметрии и эксцесса не должны превышать своих двукратных средних квадратических отклонений, т.е.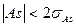 
и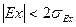 
. Эти средние квадратические отклонения вычисляются по формулам:
;
.
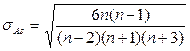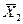Дата добавления: 2019-04-03; просмотров: 522;