Регрессионный анализ.
Изучение корреляционной связи начинается с регрессионного анализа, который решает проблему установления формы связи или вида уравнения регрессии и определения параметров уравнения регрессии.
Различают уравнения простой (парной) регрессии (когда один х соответствует у) и множественной (многофакторной) регрессии (когда результативный признак у связан с несколькими факторными признаками х).
Уравнение регрессии показывает, как в среднем изменяется у при изменении какого-либо хі и имеет вид:
У(х) = f(х1,х2……хn).
Наиболее часто для характеристики корреляционной связи используют такие вид уравнений парной регрессии:
- линейное 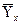 = а0+ a1 x;
= а0+ a1 x;
- гиперболическое 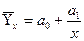 ;
;
- параболическое 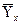 = а0+ а1 x + а1 x2 і т.д.
= а0+ а1 x + а1 x2 і т.д.
где а0, а1 – параметры уравнений регрессии, которые необходимо определить.
Параметр а0 показывает усредненное влияние на результативный признак факторов, которые не учтены.
Параметр а1 показывает насколько изменяется в среднем значение результативного признака при увеличении факторного признака на единицу.
Параметры в уравнениях регрессии определяются методом наименьших квадратов, суть которого в минимизации суммы квадратов отклонений фактических значений результативного показателя от расчетных значений.
Система нормальных уравнений для нахождения параметров линейной регрессии методом наименьших квадратов имеет такой вид:
па0 + а1 x= у;
а0 x + а1 x2 = xу,
где n – объем исследуемой совокупности (число единиц наблюдения).
Например, имеются данные, характеризующие деловую активность акционерных обществ закрытого типа (АОЗТ): прибыль (млн. р.) и затраты на 1 р. произведенной продукции (коп). (табл.8.1).
Предположим наличие линейной зависимости между анализируемыми признаками. Система нормальных уравнений для данного примера имеет вид:
па0 + а1 x= у;
а0 x + а1 x2 = xу,
Подставив данные, рассчитанные в табл.8.1. получим:
6а0 + 502а1 = 4466;
502 а0 + 42280 а1 = 362404.
Таблица 8.1
Расчетные данные для определения параметров линейного уравнения регрессии
| № | Затраты на 1 р. произведенной продукции, коп. , х | Прибыль, тыс. р., у | x2 | ху | __ x |
| 5 929 5 929 5 561 6 724 7 921 9 216 | 82 390 77 077 63 909 63 878 53 934 21 216 | 1 016 1 016 | |||
| Итого | 4 466 | 42 280 | 362 404 | 4 466 |
Решив систему уравнений получим: а0 = 4153,88; а1 = - 40,75
Таким образом, Ух = 4153,88 - 40,75x.
Если связь между признаками х и у является криволинейной и описывается уравнением параболы второго порядка:
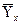 = а0+ а1 x + а2 x2
= а0+ а1 x + а2 x2
задача сводится к определению неизвестных параметров: а0, а1, а2, а система нормальных уравнений имеет вид:
па0 + а1 x + а2 x2 = у;
а0 x+ а1 x2 + а2 x3 = уx;
а0 x2 + а1 x3 + а2 x4 = уx2.
Оценка обратной зависимости между х и у, когда при увеличении (уменьшении) х уменьшается (увеличивается) значение результативного признака у, может быть осуществлена на основе уравнения гиперболы:
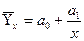 .
.
Систему нормальных уравнений для нахождения параметров гиперболы можно представить следующим образом:
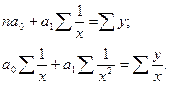
Наиболее сложным этапом, который завершает регрессионный анализ, является интерпретация уравнения, т.е. перевод его с языка статистики и математики на язык экономиста.
С целью расширения возможностей экономического анализа используется коэффициент эластичности, который определяется по формуле:
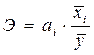 ,
,
где xі - среднее значение соответствующего факторного признака;
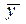 - среднее значение результативного признака;
- среднее значение результативного признака;
аі - коэффициент регрессии при соответствующем факторном признаке.
Коэффициент эластичности показывает, на сколько процентов в бреднем изменится значение результативного признака при изменении факторного признака на 1 %.
Дата добавления: 2019-04-03; просмотров: 536;
