Корреляционный анализ.

После выбора вида уравнения регрессии и нахождения его параметров приступают к оценке тесноты и значимости (существенности) связи.

Тесноту святи оценивают с помощью коэффициентов детерминации, корреляции (корреляционного отношения).

Коэффициент детерминации показывает, в какой степени вариация результативного признака у определяется вариацией факторного признака х. Он используется как при линейной, так и при нелинейной связи между признаками и в случае парной регрессии рассчитывается по формуле:

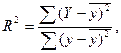
где у – фактические значения результативного признака;

У – теоретические значения результативного признака (по линии регрессии).

Коэффициент детерминации принимает значения от 0 до 1. Чем ближе он к одинице, тем теснее связь между признаками; если коэффициент детерминации равен 0 линейная связь между показателями отсутствует; если равен 1 - не существует корреляционной связи между признаками.

Коэффициент корреляции (корреляционное отношение) показывает насколько значительным является влияние фактора х на у и рассчитывается по формуле:

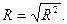
Он находится в диапазоне от 0 до1; чем ближе к единице, тем теснее корреляционная связь между признаками.

В случае линейной связи между х и улинейный коэффициент корреляции рассчитывается по формуле:

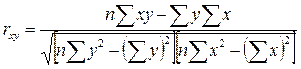
Линейный коэффициент корреляции изменяется в пределах от -1 до 1: -1 r 1.

После установления тесноты связи дают оценку значимости связи между признаками. Под термином «значимость связи» понимают оценку отклонений выборочных переменных от своих значений в генеральной совокупности с помощью статистических критериев. Оценку значимости связи осуществляют с использованием F-критерия Фишера и t-критерия Стьюдента.

Для парной регрессии (линейной и нелинейной) F-критерий Фишера рассчитывается по формуле:

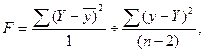
где 1, (n-2) – число степеней свободы числителя и знаменателя зависимости.

«Степень свободы» - целое число, которое показывает сколько независимых элементов информации в переменных у необходимо для суммы квадрата (это поясняет соответствующую дисперсию: общую, среднюю из групповых, межгрупповую).

Теоретическое значение F сравнивают с табличным (критическим) значением Fтабл, которое выбирают из справочных математических таблиц F-критерияФишера в зависимости от степеней свободы 1, (n-2) и принятого уровня значимости 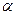. Чаще всего в статистико-экономических исследованиях используют такие уровни значимости, как 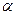=0,05 и 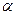=0,01. Если F> Fтабл, то выборочная совокупность и связь между признаками являются значительными.

Для парной линейной регрессии при r=R расчетные значения t –критерия Стьюдента определяются по формуле:

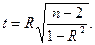
Критерий Стьюдента дает оценку значимости коэффициента корреляции R исущественности связи между признаками.

Рассчитанное по формуле теоретическое значение t –критерия Стьюдента сравнивают с табличным для соответствующего числа степеней свободы и принятого уровня значимости 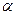. Табличное значение критерия Стьюдента выбирается из справочных математических таблиц. Если t>tтабл,то линейный коэффициент корреляции считается значимым при характеристике генеральной совокупности.