Корреляционный анализ
В реальном мире многие явления природы происходят в обстановке действия многочисленных факторов, влияние каждого из них ничтожно, а число их велико. В этом случае возникает статистическая связь между случайными величинами, т.е. случайная переменная реагирует на изменение другой переменной изменением своего ряда распределения. В результате , она . переходит не в определенное состояние, а в одно из возможных своих состояний. Для изучения статистической зависимости нужно знать аналитический вид двумерного распределения. Нахождение аналитического вида двумерного распределения по выборке ограниченного объема громоздко и может привести к значительным ошибкам. Поэтому на практике при исследовании зависимостей между случайными переменными 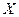 и
и 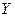 ограничиваются изучением зависимости между одной из них и условным математическим ожиданием другой. Знание статистической зависимости позволяет прогнозировать, что значение зависимой случайной переменной будет находиться в некотором интервале, если независимая переменная примет определенное значение. С помощью вероятностных методов можно вычислить вероятность того, что ошибка прогноза не выйдет за определенные границы.
ограничиваются изучением зависимости между одной из них и условным математическим ожиданием другой. Знание статистической зависимости позволяет прогнозировать, что значение зависимой случайной переменной будет находиться в некотором интервале, если независимая переменная примет определенное значение. С помощью вероятностных методов можно вычислить вероятность того, что ошибка прогноза не выйдет за определенные границы.
При изучении статистических зависимостей форму связи можно характеризовать функцией регрессии (линейной, квадратной, показательной и т.д.)
Кривой регрессии 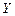 на
на 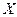 называется условное среднее значение случайной переменной
называется условное среднее значение случайной переменной 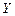 как функция
как функция 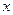 и некоторого числа параметров, которые находятся методом наименьших квадратов по наблюденным значениям двумерной случайной величины
и некоторого числа параметров, которые находятся методом наименьших квадратов по наблюденным значениям двумерной случайной величины 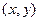 . Эта кривая называется также эмпирическим уравнением регрессии или просто уравнением регрессии.
. Эта кривая называется также эмпирическим уравнением регрессии или просто уравнением регрессии.
Статистические связи между переменными можно изучать методом корреляционного и регрессионного анализа. Основная задача корреляционного анализа – выявление связи между случайными переменными путем точечной и интервальной оценки парных коэффициентов корреляции, вычисления функции регрессии одной случайной величины на другую. Корреляционный анализ статистических данных включает следующие этапы: 1) построение корреляционного поля и составление корреляционной таблицы; 2) вычисление выборочных коэффициентов корреляции и корреляционных отношений; 3) проверка статистической гипотезы значимости связи.
Поле корреляции. Корреляционная таблица
Рассмотрим простейший случай корреляционного анализа – двумерную модель. Пусть 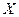 и
и 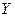 случайные переменные, Пару случайных чисел
случайные переменные, Пару случайных чисел
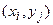 можно изобразить графически в виде точки с координатами
можно изобразить графически в виде точки с координатами 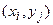 . Аналогично можно изобразить всю выборку.
. Аналогично можно изобразить всю выборку.
Декартова плоскость с нанесенными на нее точками с координатами 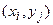 , являющимися значениями случайного вектора, называется корреляционным полем .
, являющимися значениями случайного вектора, называется корреляционным полем .
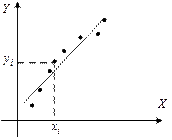
По виду корреляционного поля иногда можно судить о виде зависимости между случайными величинами 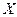 и
и 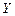 , если она существует.
, если она существует.
В данном случае представлено корреляционное поле для дискретного случайного вектора. При большом объеме выборки построение поля корреляции становится очень громоздкой задачей. Задача упрощается, если выборку упорядочить, т.е. переменные сгруппировать. В результате получится сгруппированный статистический ряд. Сгруппированный ряд может быть дискретным или интервальным. Сгруппированному ряду соответствует корреляционная таблица. Пусть, например  - объем выполненных работ,
- объем выполненных работ, 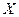 – накладные расходы. Для случайного вектора (
– накладные расходы. Для случайного вектора ( 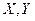 ) получена выборка, которую можно представить с помощью корреляционной таблицы
) получена выборка, которую можно представить с помощью корреляционной таблицы
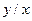
| 1-2 1.5 | 2-3 2.5 | 3-4 3.5 | 4-5 4.5 | 5-6 5.5 | 6-7 6.5 | 7-8 7.5 | 8-9 8.5 | 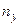
|
| 10-20 | |||||||||
| 20-30 | |||||||||
| 30-40 | |||||||||
| 40-50 | |||||||||
| 50-60 | |||||||||
| 60-70 | |||||||||
| 70-80 | |||||||||
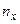
|
Эта таблица построена на основе интервального ряда. В первой строке и первом столбце таблицы помещают интервалы изменения 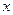 и
и 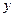 и значения середин интервалов. В ячейки, образованные пересечением строк и столбцов помещают частоты
и значения середин интервалов. В ячейки, образованные пересечением строк и столбцов помещают частоты 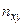 попадания пар значений
попадания пар значений 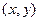 в соответствующие интервалы. В последней строке и последнем столбце находятся значения
в соответствующие интервалы. В последней строке и последнем столбце находятся значения 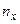 и
и 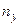 - суммы
- суммы 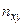 по соответствующим столбцу и строке , где
по соответствующим столбцу и строке , где 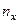 – суммарная частота наблюдаемого значения признака
– суммарная частота наблюдаемого значения признака 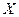 при всех значениях
при всех значениях 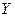 ,
, 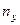 – суммарная частота наблюдаемого значения признака
– суммарная частота наблюдаемого значения признака 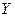 при всех значениях
при всех значениях 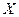 ,
, 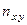 –частота появления пары значений признаков
–частота появления пары значений признаков 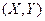 .При этом выполняются равенства
.При этом выполняются равенства
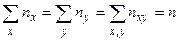 , (3.1)
, (3.1)
где 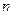 - объем выборки.
- объем выборки.
Вычислим статистические оценки параметров распределения случайного вектора. Статистической оценкой математического ожидания является среднее арифметическое, а статистической оценкой дисперсии является статистическая дисперсия. Вычисление этих величин в данном случае проводится по формулам
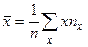 ,
, 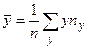 , (3.2)
, (3.2)
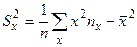 ,
, 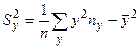 . (3.3)
. (3.3)
Оценкой коэффициента корреляции является выборочный коэффициент корреляции, который определяется равенством
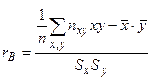 (3.4)
(3.4)
В данном примере
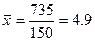 ,
, 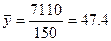
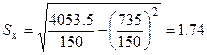 ,
, 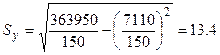
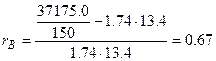 .
.
Величина выборочного коэффициента корреляции не зависит от порядка следования переменных, т.е. 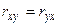 , поэтому выборочный коэффициент корреляции обозначают просто
, поэтому выборочный коэффициент корреляции обозначают просто 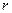 .
.
Если генеральная совокупность имеет нормальное распределение, т. е. совместная функция распределения 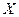 и
и 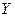 подчиняется нормальному закону,
подчиняется нормальному закону,
то функция регрессии линейны. Функция регрессии 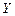 на
на 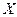 имеет вид
имеет вид
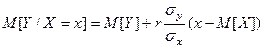 , (3.5)
, (3.5)
а функция регрессии 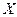 на
на 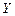 имеет вид
имеет вид
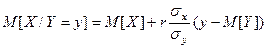 . (3.6)
. (3.6)
Выражения 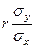 и
и 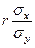 называются коэффициентами регрессии.
называются коэффициентами регрессии.
Уравнения регрессии 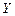 на
на 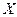 и
и 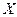 на
на 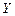 имеют вид
имеют вид
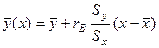 ,
, 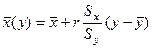 (3.7)
(3.7)
В данном примере уравнение регрессии 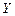 на
на 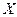
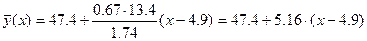 ,
,
уравнение регрессии 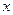 на
на 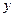
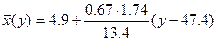 .
.
Полученные уравнения регрессии показывают, как в среднем изменяется 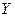
(или 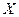 ) в зависимости от изменения аргумента
) в зависимости от изменения аргумента 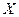 (или
(или 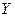 ).
).
Проверка гипотезы о значимости коэффициента корреляции.
Выборочный коэффициент корреляции является точечной оценкой коэффициента корреляции. Он служит для оценки силы линейной связи между 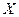 и
и 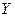 . Равенство нулю выборочного коэффициента корреляции еще не свидетельствует о равенстве нулю самого коэффициента корреляции, а, следовательно, о некоррелированности случайных величин
. Равенство нулю выборочного коэффициента корреляции еще не свидетельствует о равенстве нулю самого коэффициента корреляции, а, следовательно, о некоррелированности случайных величин 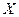 и
и 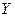 . Чтобы выяснить, находятся ли случайные величины в корреляционной зависимости, нужно проверить значимость выборочного коэффициента корреляции
. Чтобы выяснить, находятся ли случайные величины в корреляционной зависимости, нужно проверить значимость выборочного коэффициента корреляции 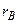 , т.е. установить, достаточна ли его величина для обоснованного вывода о наличии корреляционной связи. Для этого проверяют нулевую гипотезу
, т.е. установить, достаточна ли его величина для обоснованного вывода о наличии корреляционной связи. Для этого проверяют нулевую гипотезу 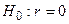 , т.е. случайные величины в генеральной совокупности не коррелированы. Альтернативная гипотеза
, т.е. случайные величины в генеральной совокупности не коррелированы. Альтернативная гипотеза 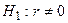 . Предполагая, что имеется двумерное нормальное распределение случайных переменных, вычисляют статистику
. Предполагая, что имеется двумерное нормальное распределение случайных переменных, вычисляют статистику
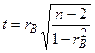 , (3.8)
, (3.8)
которая имеет распределение Стьюдента с 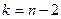 степенями свободы. Для проверки нулевой гипотезы по уровню значимости
степенями свободы. Для проверки нулевой гипотезы по уровню значимости 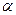 и числу степеней свободы
и числу степеней свободы 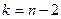 находят по таблицам распределения Стьюдента критическое значение
находят по таблицам распределения Стьюдента критическое значение 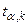 , удовлетворяющее условию
, удовлетворяющее условию 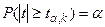 . Если
. Если 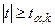 , то нулевую гипотезу об отсутствии корреляционной связи между переменными
, то нулевую гипотезу об отсутствии корреляционной связи между переменными 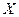 и
и 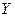 следует отвергнуть. В этом случае переменные являются зависимыми. Если
следует отвергнуть. В этом случае переменные являются зависимыми. Если 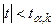 , то нет оснований отвергать нулевую гипотезу.
, то нет оснований отвергать нулевую гипотезу.
В нашем примере зададим 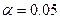 . По формуле (3.8) найдем статистику
. По формуле (3.8) найдем статистику 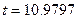 . Из таблиц распределения критических точек Стьюдента по заданному уровню значимости
. Из таблиц распределения критических точек Стьюдента по заданному уровню значимости 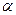 и числу степеней свободы
и числу степеней свободы 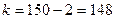 найдем критическую точку
найдем критическую точку 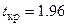 . Так как
. Так как 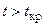 , то нулевая гипотеза отвергается. Рассматриваемые случайные величины являются коррелированными и, следовательно, зависимыми.
, то нулевая гипотеза отвергается. Рассматриваемые случайные величины являются коррелированными и, следовательно, зависимыми.
В случае значимого выборочного коэффициента корреляции можно построить доверительный интервал для коэффициента корреляции.
Плотность вероятности выборочного коэффициента корреляции имеет сложный вид. Поэтому прибегают к специально подобранным функциям от выборочного коэффициента корреляции, которые сводятся хорошо изученным распределениям, например, к нормальному или Стьюдента.
Чаще всего используют преобразование Фишера.
По выборочному коэффициенту корреляции вычисляют статистику 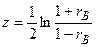 . Отсюда
. Отсюда 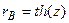 .
.
Распределение статистики 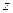 хорошо аппроксимируется нормальным распределением с параметрами
хорошо аппроксимируется нормальным распределением с параметрами 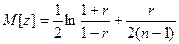 и
и 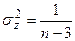 .
.
В этом случае доверительный интервал для 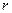 имеет вид
имеет вид 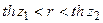 . Величины
. Величины 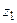 и
и 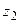 находят по таблицам
находят по таблицам
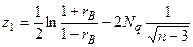
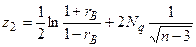
где 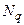 – нормированная функция Лапласа для
– нормированная функция Лапласа для 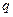 % доверительного интервала.
% доверительного интервала.
Если коэффициент корреляции значим, то коэффициенты регрессии значимо отличаются от нуля. Интервальные оценки для них имеют вид
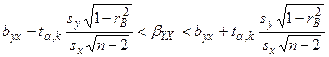
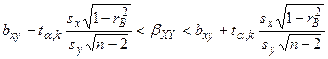
где 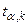 имеет распределение Стьюдента с
имеет распределение Стьюдента с 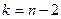 степенями свободы.Регрессионный анализ
степенями свободы.Регрессионный анализ
Основная задача регрессионного анализа– изучение зависимости между результативным признаком 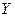 и наблюдавшимся признаком
и наблюдавшимся признаком 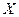 , оценка функции регрессии. Рассмотрим линейный регрессионный анализ в котором условное математическое ожидание можно представить в виде линейной функции от оцениваемых параметров
, оценка функции регрессии. Рассмотрим линейный регрессионный анализ в котором условное математическое ожидание можно представить в виде линейной функции от оцениваемых параметров
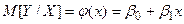 . (3.9)
. (3.9)
Это выражение называется функцией регрессии или модельным уравнением регрессии. Параметры 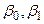 называются коэффициентами регрессии. Оценки этих параметров обозначим
называются коэффициентами регрессии. Оценки этих параметров обозначим 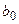 и
и 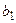 . Подставляя эти оценки в формулу (9) вместо параметров, получим линейное уравнение регрессии
. Подставляя эти оценки в формулу (9) вместо параметров, получим линейное уравнение регрессии
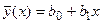 , (3.10)
, (3.10)
коэффициенты которого найдем методом наименьших квадратов из условия минимума суммы квадратов отклонений измеренных значений результативного признака 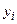 от вычисленных по уравнению регрессии
от вычисленных по уравнению регрессии 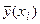 , т. е. условия минимума величины
, т. е. условия минимума величины
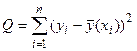 (3.11)
(3.11)
Подставляя в (3.11) выражение (3.10), получим
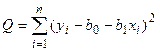 (3.12)
(3.12)
В соответствии с необходимым условием минимума функции приравняем нулю частные производные функции 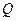 по переменным
по переменным 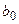 и
и 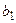 . В результате получим систему нормальных уравнений
. В результате получим систему нормальных уравнений
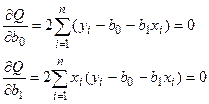 (3.13)
(3.13)
После упрощения система уравнений (3.13) приводится к виду
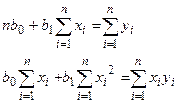 (14)
(14)
Оценки, полученные по методу наименьших квадратов, обладают наименьшей дисперсией в классе линейных оценок. В случае, когда наблюдавшиеся данные представлены корреляционной таблицей, нужно произвести следующие замены в уравнениях (3.14)
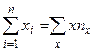 ,
, 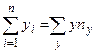 ,
, 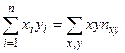 ,
,
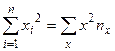 (3.15)
(3.15)
где 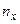 ,
, 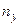 ,
, 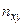 соответствующие частоты:
соответствующие частоты:
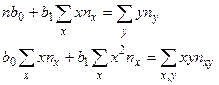 (3.16)
(3.16)
Систему уравнений (3.16) можно переписать в виде
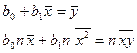
Решая эту систему, найдем значения параметров 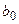 и
и 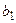
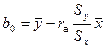 ,
, 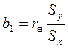
и уравнение регрессии
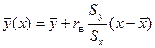 .
.
В примере 1 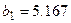 ,
, 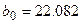 . Уравнение регрессии имеет вид
. Уравнение регрессии имеет вид
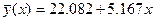 .
.
Дата добавления: 2019-10-16; просмотров: 1804;
