Корреляционное отношение
Корреляционное отношение определяется равенством
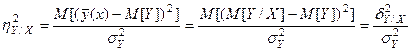 ,
,
где 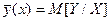 , которое в случае линейной регрессии имеет вид
, которое в случае линейной регрессии имеет вид 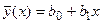 , а в случае квадратичной регрессии имеет вид
, а в случае квадратичной регрессии имеет вид 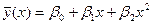 .
.
Корреляционное отношение можно представить формулой
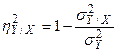 .
.
При вычислении корреляционного отношения по выборочным данным получается выборочное корреляционное отношение 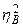 . В этом случае вместо дисперсий используются их статистические оценки. Тогда
. В этом случае вместо дисперсий используются их статистические оценки. Тогда
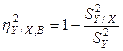 (3.19)
(3.19)
где
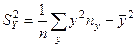 ,
, 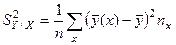 .
.
Напомним, что 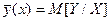 (
( 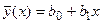 в случае линейной регрессии,
в случае линейной регрессии, 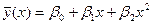 в случае квадратичной регрессии)
в случае квадратичной регрессии)
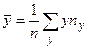 .
.
Выборочное значение 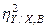 вычисляется по данным корреляционной таблицы с помощью формулы
вычисляется по данным корреляционной таблицы с помощью формулы
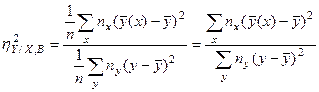 ,
,
где числитель характеризует рассеяние условных средних значений 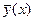 относительно безусловного среднего арифметического
относительно безусловного среднего арифметического 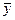 .
.
Проверка значимости корреляционного отношения основана на том, что критерий 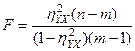 имеет распределение Фишера с
имеет распределение Фишера с 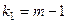 ,
, 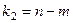 степенями свободы. Здесь
степенями свободы. Здесь 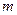 - число интервалов группировки значений случайной величины
- число интервалов группировки значений случайной величины 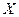 . В качестве основной гипотезы обычно принимают отсутствие корреляционной связи
. В качестве основной гипотезы обычно принимают отсутствие корреляционной связи 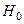 :
: 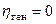 при альтернативной
при альтернативной 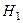 :
: 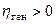 .
.
Дата добавления: 2019-10-16; просмотров: 556;
