Вероятностью события называется отношение числа благоприятных для него исходов к числу всех равновозможных исходов
Можно записать в тетрадь такое правило
ВЕРОЯТНОСТЬ = число благоприятных исходов : число равновозможных исходов
2 Решение задач на нахождение вероятностей
32
№1 В коробке находится 10 белых, 8 красных, 12 синих шаров. Наугад выбирают 1 шар. Какова вероятность того, что а) шар белый, б) шар красный, в) шар синий.
Решение
10 + 8 + 12 = 30 шаров всего - у каждого есть шанс быть выбранным – значит число равновозможных исходов равно 30
1) событие А - шар белый , т. к. белых шаров 10, то это число благоприятных
исходов , Р(А)- вероятность события А , Р(А) =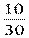 
= 
2) Р(Б) –вероятность того , что шар красный , Р(Б) =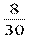 
= 
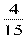
3) Р(В)- вероятность того, шар синий, Р(В) =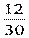 
= 
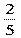
№2 Из 25 билетов по геометрии ученик подготовил 11 первых и 8 последних. Какова вероятность того, что на экзамене ему достанется билет, который он не подготовил.
Решение
25 – число равновозможных исходов
25 – ( 11 + 8) = 6 – число благоприятных исходов
Р(А)=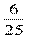 
= 0,24
№3. В слове ВЕРОЯТНОСТЬ наугад взяли 1 букву. Какова вероятность того, что
1) буква будет гласной; 2) это будет ь; 3) это будет буква о.
Решение
1) В слове ВЕРОЯТНОСТЬ 11 букв, значит 11- число равновозможных исходов,
4 буквы гласные, значит 4 благоприятных исхода, тогда Р(А) =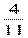 
2) Буква ь одна, значит 1 благоприятный исход, тогда Р(В) =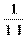 
3) В данном слове две буквы о, значит 2 благоприятных исхода, тогда Р(С)=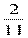 
№4. На 1000 телевизоров в среднем приходится 7 бракованных. Какова вероятность купить исправный телевизор?
Решение
1000 - - число равновозможных исходов
1000 - 7 = 993 исправных телевизора – это число благоприятных исходов
Р(А) = 
= 0,993 _
Примеры задач
В10 по математике:
Брошена игральная кость. Какова вероятность того, что выпадет чётное число очков?
1, 3, 5 — нечетные числа; 2, 4, 6 — четные. Число возможных исходов при бросании игральной кости 6. Число благоприятных исходов 3 (выпадение двойки, четвёрки или шестёрки). Таким образом, вероятность выпадения четного числа очков равна три к шести или 0,5.
Ответ: 0,5
Брошена игральная кость. Какова вероятность того, что выпадет число меньше 4?
Другими словами, какова вероятность того, что выпадет либо единица, либо двойка, либо тройка? Число возможных исходов 6. Число благоприятных исходов 3 (выпадение единицы, двойки или тройки). Таким образом, вероятность выпадения числа меньшего четырёх будет 3 к 6 или 3/6=0,5.
Ответ: 0,5
В ящике 6 белых и 4 чёрных шара. Какова вероятность того, что первый наудачу выбранный шар окажется белым?
Всего шаров 10, значит число возможных исходов 10. Число благоприятных исходов 6 (в ящике 6 белых шаров). Вероятность того, что первый выбранный шар окажется белым 6 к 10, то есть 6/10=0,6
Ответ: 0,6
Набирая номер телефона, абонент забыл последнюю цифру. Какова вероятность того, что он правильно дозвонится, набрав последнюю цифру наугад?
Абоненту нужно выбрать одну из десяти цифр, то есть число возможных исходов 10. Число благоприятных исходов 1 (верной может быть только одна цифра). Вероятность того, что он правильно дозвонится равна 1 к 10 или 0,1.
Ответ: 0,1
Ученика попросили назвать число от 1 до 100. Какова вероятность того, что он назовёт число 56?
Число возможных исходов 100 (сто чисел). Верно названное число одно это 56, значит благоприятный исход один. Вероятность того, что он назовёт число 56 будет один к ста или 0,01.
Ответ: 0,01
Ученика попросили назвать число от 1 до 100. Какова вероятность того, что он назовёт число кратное пяти?
Число возможных исходов 100 (сто чисел). Чисел кратных пяти двадцать (перечислим):5,10,15,20,25,30,35,40,45,50,55,60,65,70,75,80,85,90,95,100. То есть число благоприятных исходов 20. Вероятность того, что ученик назовёт число кратное пяти равна 20 к 100 или 20/100=0,2.
Ответ: 0,2
Ученика попросили назвать число от 1 до 100. Какова вероятность того, что он назовёт число, принадлежащее промежутку от 5 до 20 включительно?
Число возможных исходов 100. Число благоприятных исходов 16: это числа от 5 до 20 (5,6…..19,20), причём 5 и 20 входят в промежуток (в условии сказано «от 5 до 20 включительно»). Искомая вероятность равна 16/100.
Ответ: 0,16
В фирме такси в данный момент свободно 10 машин: 5 чёрных, 1 жёлтая и 4 зелёных. На вызов выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет жёлтое такси.
Возможное число исходов 10. Число благоприятных исходов 1 (жёлтая машина одна). Искомая вероятность равна 1 к 10 или 0,1.
Ответ: 0,1
Валя выбирает трёхзначное число. Найдите вероятность того, что оно делится на 51.
Число возможных исходов это количество трёхзначных чисел. Их существует от 100 до 999, быстрее всего их можно посчитать так: 1000-1-99=900 (исключаем тысячу и числа от 1 до 99). То есть число всевозможных исходов: 900. Найдем, сколько трехзначных чисел делится на 51. Если мы поделим 999 - самое большое трехзначное число - на 51, то получим приблизительно 19 целых пятьдесят восемь сотых. То есть в 999 вмещается 19 чисел, кратных 51. Но среди них есть и само число 51, которое не является трехзначным. А значит трехзначных чисел, делящихся на 51 - 18. Число благоприятных исходов 18. Вероятность искомого события равна 18 к 900, или 18/900=0,02.
Ответ: 0,02
При двукратном бросании игрального кубика в сумме выпало 6 очков. Найдите вероятность того, что первый раз выпало меньше трёх очков.
Сумму в шесть очков можно получить следующими способами (переберём варианты): 1+5, 2+4, 3+3, 4+2, 5+1 - всего их пять, это и есть число возможных исходов. Из представленных вариантов также видно, что менее трёх очков при первом броске может выпасть только в двух случаях. Искомая вероятность равна 2 к 5 или 0,4.
Ответ: 0,4
Дата добавления: 2017-12-05; просмотров: 1131;