Вероятность противоположного события
Несколько событий в данном опыте образуют полную группу, если в результате опыта обязательно должно появиться хотя бы одно из этих событий, Отсюда следует, что сумма событий полной группы есть достоверное событие, вероятность которого равна единице.
Если события, образующие полную группу, попарно несовместны, то в результате опыта появится одно и только одно из этих событий.
Для суммы таких событий справедлива формула
P(A1+A2+….+An) = P(A1)+P(A2)+….+P(An) = 1.
Теорема: Два противоположных друг другу события образуют полную группу:
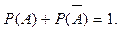
Пример: В партии содержится 20 деталей, среди которых 4 нестандартных. Для контроля взяли наудачу 3 детали. Найти вероятность того, что хотя бы одна из взятых деталей нестандартна.
Решение: Пусть событие А – хотя бы одна из взятых деталей окажется нестандартной. Рассмотрим событие 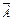 , противоположное событию А:
, противоположное событию А:
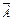 - среди взятых деталей нет нестандартных. Вычислим вероятность события
- среди взятых деталей нет нестандартных. Вычислим вероятность события 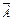 :
: 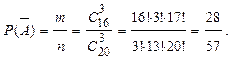
Теперь вычислим вероятность искомого события:
P(A) = 1- 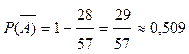 .
.
Пример: Перегорела одна из пяти электроламп, включенных в сеть последовательно. С целью устранения повреждения наудачу выбранную лампочку заменяют годной, после чего сразу проверяется исправность линии. Если повреждение не устранено, то заменяется другая лампочка. Найти вероятность того, что повреждение будет устранено только после замены третьей лампочки.
Решение: Пусть событие А – повреждение будет исправлено после замены третьей лампы.
Рассмотрим следующие три события:
А1 – первая замененная лампа оказалась перегоревшей;
А2 – вторая замененная лампа оказалась перегоревшей;
А3 – третья замененная лампа оказалась перегоревшей.
Тогда: А = 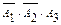
Поскольку события 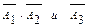 зависимы, то
зависимы, то 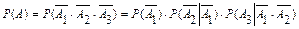
Вероятность события 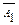 есть вероятность того, что первая замененная лампа оказалась исправной
есть вероятность того, что первая замененная лампа оказалась исправной 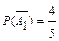 .
.
Условная вероятность 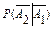 - вероятность того, что вторая замененная лампа оказалась исправной, если известно, что первая замененная лампа также исправна.
- вероятность того, что вторая замененная лампа оказалась исправной, если известно, что первая замененная лампа также исправна.
Поэтому 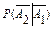 =
=  .
.
Наконец, условная вероятность 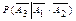 есть вероятность того, что третья замененная лампа оказалась перегоревшей, если известно, что первая и вторая замененные лампы были исправными.
есть вероятность того, что третья замененная лампа оказалась перегоревшей, если известно, что первая и вторая замененные лампы были исправными.
Откуда 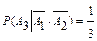 .
.
Теперь подсчитаем искомую вероятность: P(A)= 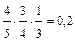
Пример: Вероятности того, что деталь нужного вида находится в первом, втором, третьем ящике соответственно равны 0,7; 0,8; 0,9. Найти вероятность того, что деталь содержится не менее, чем в двух ящиках.
Решение: Пусть событие А – деталь нужного вида находится не менее, чем в двух ящиках. Рассмотрим следующие три события:
А1 – деталь нужного вида имеется в 1-ом ящике;
А2 – деталь нужного вида имеется во 2-ом ящике;
А3 - деталь нужного вида имеется в 3-ем ящике.
Событие B1= 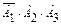 заключается в том, что нужного вида деталь имеется во 2-ом и 3-ем ящиках, но ее нет в 1-ом ящике. События имеется во 2-ом и 3-ем независимы, поэтому
заключается в том, что нужного вида деталь имеется во 2-ом и 3-ем ящиках, но ее нет в 1-ом ящике. События имеется во 2-ом и 3-ем независимы, поэтому
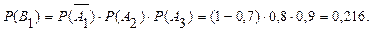
Событие 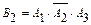 заключается в том, что нужного вида деталь имеется в 1-ом и в 3-ем ящиках, но ее нет во 2-ом ящике.
заключается в том, что нужного вида деталь имеется в 1-ом и в 3-ем ящиках, но ее нет во 2-ом ящике.
Событие B3=A1 ,A2 , 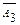 заключается в том, что нужного вида деталь имеется в 1-ом и 2-ом ящиках, но ее нет в 3-ем ящике.
заключается в том, что нужного вида деталь имеется в 1-ом и 2-ом ящиках, но ее нет в 3-ем ящике.
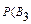 )=P(A1) ,P(A2) ,P(
)=P(A1) ,P(A2) ,P( 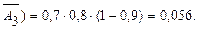
Наконец, событие B4=A1 ,A2 ,A3 заключается в том, что нужного вида деталь имеется и в 1-ом, и во 2-ом, и в 3-ем ящиках.
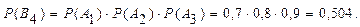
Событие А произойдет тогда, когда произойдет одно из событий:
или В1, или В2, или В3, или В4. Поэтому А=В1+В2+В3+В4.
Поскольку события В1, В2, В3, В4 несовместны, то
P(A)=P(В1)+P(В2)+P(B3)+P(B4).
Вычисляем:
P(A)=0,216+0,126+0,056+0,504=0,902.
Варианты заданий
Решить задачи
Дата добавления: 2017-06-02; просмотров: 1487;
