Примеры использования классического определение вероятности
Пусть некоторый опыт может приводить лишь к одному из конечного множества результатов. Эти результаты будем называть элементарными исходами. Предположим, что элементарные исходы удовлетворяют следующим условиям:
1) образуют полную группу, т.е. в каждом испытании обязан появиться какой-нибудь из этих исходов;
2) попарно несовместны, т.е. два различных элементарных исхода не могут появиться в одном испытании;
3) равновозможные, т.е. шансы на появление у всех элементарных исходов одинаковы.
В этих условиях может использоваться классическое определение вероятности.
Определение: Элементарные исходы, в которых появляются интересующее нас событие, называются благоприятными этому событию.
Определение: Вероятностью события А называются число P(А), равное отношению числа исходов испытания, благоприятствующих событию А к общему числу исходов:
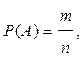 где n – общее число исходов испытания, m – число исходов, благоприятствующих событию А.
где n – общее число исходов испытания, m – число исходов, благоприятствующих событию А.
Пример: Бросается один раз игральная кость. Какова вероятность выпадения нечетного числа очков?
Решение: Опыт состоит в бросании игральной кости 1 раз и наблюдении за числом очков, появившихся на верхней грани.
Все исходы опыта: 1, 2, 3, 4, 5, 6.
Число всех исходов: n = 6.
Рассмотрим событие А – выпало нечетное число очков. Исходы благоприятствующие А: 1, 3, 5.
Число исходов, благоприятствующих А : m = 3
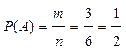 .
.
Пример: Ребенок играет с шестью буквами разрезной азбуки А, В, К, М, О, С. Какова вероятность того, что при случайном расположении букв в ряд получится слово «МОСКВА»?
Решение: Опыт состоит в случайном расположении шести букв в ряд. Все исходы опыта – множество перестановок из шести различных букв.
Число всех исходов: n = P6=6! = 1.2.3.4 .5.6=720.
Рассмотрим событие А – при случайном расположении шести букв в ряд получено слово «МОСКВА». Очевидно, что такое расположение букв единственно, т.е. m=1. Найдем вероятность события А: P(A)= 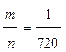 .
.
Пример: В ящике находится 20 деталей, из них 8 бракованных. Из ящика наудачу извлекают 5 деталей. Найти вероятность того, что среди них окажутся две бракованные детали.
Решение: Опыт состоит в выборе наудачу 5 деталей из 20. Все исходы опыта – множество сочетаний из 20 деталей (находящихся в ящике) по 5.
Число всех исходов опыта n= 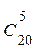 =
= 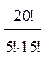
Рассмотрим событие А – среди 5 деталей, извлеченных из ящика, две бракованные.
Если среди 5 деталей две бракованные, то остальные 3 небракованные. Тогда число исходов, благоприятствующих
событию А, можно найти по принципу умножения. Нужно выполнить одно за другим два действия: из 8 бракованных выбрать 2 детали и затем из 12 небракованных выбрать 3 детали. Первое действие можно выполнить n1= 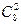 второе действие можно выполнить n2=
второе действие можно выполнить n2= 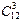 способами. Итак, m=n1.n2=
способами. Итак, m=n1.n2= 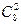
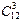 .
.
Найдем вероятность события А:
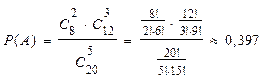
Дата добавления: 2017-06-02; просмотров: 3720;
