Задачи на классическое определение вероятности

Буквой A обозначаем событие, фигурирующее в условии задачи.

Задача.Корреспонденция разносится в 5 адресов. Разносчик забыл дома очки и разнес корреспонденцию случайным образом. Какова вероятность того, что вся корреспонденция попала к своимадресатам?

Решение. Элементарным событием является перестановка из 5 адресов. Их число равно 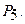По смыслу задачи все они равновероятны. Поэтому P(A)= 1/120.

Задача.Цифры 0,1,2,3 написаны на четырех карточках. Карточки расположили в случайном порядке. Какова вероятность того, что из них сложено 4-х-значное число?

Решение. Элементарным событием является перестановка из 4 карточек. Их всего 4!. Поскольку четырехзначное число не может начинаться с нуля, то событие A состоит из тех перестановок, которые начинаются с карточки с не равной нулю цифрой. Их всего 4!-3!=18. Поэтому P(A)= 18/4! =18/24=3/4.

Задача.Вхоккейном турнире участвуют 6 равных по силе команд. Каждая команда должна сыграть с каждой одну игру. У Вас есть любимая команда. Вы пришли «поболеть» на турнир на одну из игр, выбранных случайно. Какова вероятность того, что в этой игре будет играть Ваша любимая команда?

Решение. Общее число проведенных игр равно C₆²=15. Любимая команда участвует в 5 играх из 15. Поэтому P(A)= 5/15 = 1/3.

Задача. В ящике разложено 20 деталей. Известно, что 5 из них являются стандартными. Рабочий случайным образом берет 3 детали. Какова вероятность того, что хотя бы одна деталь стандартная?

Решение. Элементарным событием является сочетание из 20 деталей по 3. Количество таких сочетаний равно C₂₀³. В соответствии с решением задачи 11, число сочетаний, содержащих хотя бы одну стандартную деталь равно C₂₀³- C₁₅³=685. Поэтому P(A)=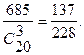

Задача. Из 7 карточек разрезной азбуки составлено слово колокол.Эти карточки рассыпали и затем собрали в случайном порядке. Какова вероятность того, что снова получится слово колокол?

Решение. На карточках имеется 3 буквы о, 2 буквы к, 2 буквы л. Поэтому, первая буква слова колокол может быть выбрана двумя способами, вторая – 3 способами, третья – 2 способами. При уже выбранных первых трех буквах четвертая буква может быть выбрана еще 2 способами (поскольку одна буква о уже выбрана). Остальные буквы могут быть выбраны только одним способом. Таким образом (см. решение задачи 12), число перестановок карточек, реализующих слово колокол равно произведению чисел 3, 2, 2, 2 т.е. равен 24. Общее число перестановок карточек равно 7!.Поэтому P(A)=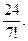

Варианты заданий

Решить задачи

1. Из ящика, в котором 10 белых и 6 черных шаров, берут наудачу 3 шара. Какова вероятность того, что один из них белый, а два черных?

2. Набирая номер телефона, абонент забыл три последние цифры, запомнив лишь, что они различные, набрал их наудачу. Найти вероятность того, что набраны нужные цифры?

3. 25 экзаменационных билетов содержат по две вопроса, которые не повторяются. Студент подготовил 45 вопросов. Какова вероятность того, что вытянутый студентом билет состоит из подготовленных им вопросов?

4. В мастерскую для ремонта поступило 15 телевизоров. Известно, что 6 из них нуждаются в общей регулировке. Мастер берет первые попавшиеся 5 телевизоров. Какова вероятность того, что 2 из них нуждаются в общей регулировке.

5. Из колоды в 52 карты берется наугад 4 карты. Найти вероятность того, что среди этих 4 карт будут представлены все четыре масти.

6. На полке в случайном порядке расставлено 40 книг, среди них находится трехтомник А.С.Пушкина. Некто взял наудачу с полки 5 книг. Найти вероятность того, что среди этих пяти книг есть трехтомник Пушкина.

7. Секретных замок содержит на общей оси 4 диска, каждый из которых разделен на 5 секторов с различными цифрами. Замок открывается только в том случае, если диски установлены так, что образуют определенное число. Найти вероятность того, что при произвольной установке дисков замок откроется.

Самостоятельная работа №4 Нахождение условных вероятностей. Вычисление вероятностей сложных событий с помощью теорем умножения и сложения вероятностей