Предельные теоремы для схемы Бернулли
Теорема Пуассона. (Отметим, что на практике эта теорема применяется при 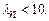 Это означает, что p должно быть очень малым числом). Пусть имеется n независимых испытаний с вероятностью р успеха в одном испытании и q- вероятностью неудачи. Тогда для любого фиксированного m справедливо соотношение
Это означает, что p должно быть очень малым числом). Пусть имеется n независимых испытаний с вероятностью р успеха в одном испытании и q- вероятностью неудачи. Тогда для любого фиксированного m справедливо соотношение
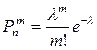 , где
, где 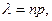
Пример.Машинистка печатает текст, который содержит 20000 знаков. Каждый знак может быть напечатан неправильно с вероятностью 0.0004. Какова вероятность того, что в тексте не менее 3 опечаток?
Решение. Если опечатку считать успехом, то к этой задаче применима схема Бернулли при p=0.0004, n=20000. Поскольку λ=np=8, то можно использовать предельную теорему Пуассона. Поэтому, искомая вероятность равна 1-Pn0- Pn1- Pn2=1-e-8- 8 e-8-(64/2) e-8= 1-41 e-8=0.986.
Пример.Монета бросается 100 раз. Найти приближенно вероятность того, что герб выпадет 40 раз. (Воспользоваться таблицей )
Решение.Если считать успехом выпадение герба, то вероятность успеха равна 1/2. Поэтому используя предельную локальную теорему Муавра-Лапласа, получим
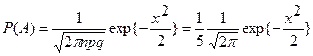 , где
, где 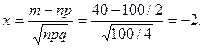
Таким образом, используя таблицы для плотности нормального распределения, получим P(A)=0.0108.
Интегральная теорема Муавра-Лапласа. Пусть имеется n независимых испытаний с вероятностью успеха p, 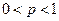 , в одном испытании и
, в одном испытании и 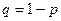 - вероятностью неудачи. Величина
- вероятностью неудачи. Величина 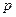 не зависит от n. Тогда .для любых вещественных чисел a<b при
не зависит от n. Тогда .для любых вещественных чисел a<b при 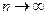
P(a< 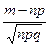 <b )=Φ(b)- Φ(a).
<b )=Φ(b)- Φ(a).
Здесь Φ(x)= 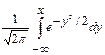 - функция Лапласа, значения которой заданы в таблицах, приведенных в большинстве задачников по вероятности и математической статистике.
- функция Лапласа, значения которой заданы в таблицах, приведенных в большинстве задачников по вероятности и математической статистике.
Пример.При рождении ребенка вероятность рождения мальчика равна 0.512. Найти вероятность того, что среди 1000 новорожденных мальчиков родится больше, чем девочек.
Решение.Пусть A – это событие, соответствующее вопросу задачи, m – это число рожденных мальчиков. Нетрудно видеть, что P(A) = P(m>500). Поскольку n=1000 можно считать достаточно большим, то применим интегральную теорему Муавра-Лапласа, согласно которой
P(A)=P( 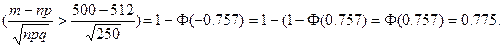
Дата добавления: 2017-06-02; просмотров: 2090;
