Теорема умножения вероятностей
Теорема: Вероятность произведения двух независимых событий равна произведению вероятностей этих событий
P(A.B) = P(A).P(B).
Пример . Какова вероятность того, что при десятикратном бросании монеты герб выпадет 10 раз ?
Решение: Пусть событие Ai — появление герба при i-м бросании. Искомая вероятность есть вероятность совмещения всех событий Ai (i=1,2,3,...,10), а так как они, очевидно, независимы в совокупности, то применяя формулу (10), имеем
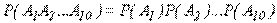
Но P(Ai)=1/2 для любого i; поэтому
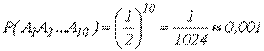
Теорема: Вероятность произведения двух зависимых событий равна произведению вероятностей одного из них на условную вероятность другого, вычисленную в предложении, что первое уже наступило.
P(A .B) = P(A).P(B½A).
Для трех зависимых событий:
P(A .B) = P(A).P(B½A).P(C½A .B).
Пример. Из урны, содержащей 3 белых и 7 черных шаров, вынимают два шара. Какова вероятность того, что оба шара окажутся белыми ?
Решение: Эта задача уже была решена в п. 3 с помощью классического определения вероятности. Решим ее, применяя формулу (5). Извлечение двух шаров равносильно последовательному их извлечению. Обозначим через А появление белого шара при первом извлечении, а через В — при втором. Событие, состоящее в появлении двух белых шаров, является совмещением событий А и В. По формуле (5) имеем
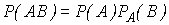
Но Р(А)=3/10; РA(В)=2/9, поскольку после того, как был вынут первый белый шар, в урне осталось 9 шаров, из которых 2 белых. Следовательно,
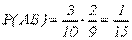
Дата добавления: 2017-06-02; просмотров: 732;
