Арифметическая операция умножения

Арифметические операции

Арифметическая операция сложения

В любой из вышеперечисленных систем исчисления можно выполнять любые арифметические операции, к которым мы привыкли в десятич­ной системе. То есть сложение, вычитание, умножение, деление. Правда, на практике никто не занимается восьмиричной и шестнадцатиричной арифметикой. Это не имеет никакого смысла. А вот арифметика в двоич­ной системе была подробно проработана.

Надо же было обучить этому электронные устройства. На самом деле правила, по которым производятся все операции в любой из систем исчисления, взяты из десятичной системы. Но при вычислениях в дво­ичной системе это выглядит немного по-другому. Возьмем, например, сложение. Как и в десятичной, так и в двоичной системе два любых числа можно сложить столбиком. Только нужно помнить, что в этой системе каждый разряд может принимать лишь два значения: либо 0, либо 1. Возьмем для примера два двоичных числа. Например, 10011001110 + 11000101110. Записываем пример сложения.

Теперь выполним сложение. Как и в десятичной системе, будем скла­дывать числа поразрядно, начиная с младшего разряда. При сложении значений каждого разряда будем учитывать следующие правила.

Правило 1.

Ноль плюс ноль — получится, естественно, ноль.

Правило 2.

Один плюс ноль и ноль плюс один дадут в результате единицу.

Правило 3.

При сложении двух единиц мы получим ноль в текущем разряде и единицу переноса в следующий разряд.

Сложив все разряды, результат запишем под чертой. Складывая зна­чение очередного разряда, не забывайте учитывать перенос из предыду­щего. При сложении двух единиц плюс перенос из предыдущего разряда получим единицу и перенос в следующий.

Арифметическая операция умножения

Умножение в двоичной системе также делается столбиком. Но в дво­ичной системе есть одна особенность, которая сильно облегчает задачу. Очевидно, что любое число, умноженное на ноль, дает в результате ноль. А число, умноженное на единицу, дает в результате само себя. Вот при­мер умножения столбиком двух двоичных чисел:

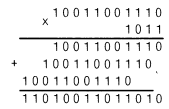
Как легко убедиться из примера, умножение в двоичной системе исчисления сводится к сложению одного и того же числа (множимого), сдвинутого относительно самого себя. Как видите, при работе с двоич­ными числами даже умножать не приходится. Достаточно уметь сдвигать разряды числа и складывать числа между собой. Это важно при построе­нии вычислительных устройств.

Простейшие микропроцессоры в составе своих команд не имеют команды умножения. Однако любой микропроцессор имеет команды сдвига и сложения. Одну команду умножения всегда можно заменить небольшим набором команд сложения и сдвига. Точно так же команду деления легко заменить сдвигом и вычитанием.