Закон нормального распределения вероятностей

Нормальное распределение широко используется в различных сферах человеческой деятельности для приближенного описания случайных явлений, так как требует знания всего двух параметров среднего значения М(Е) и стандартного отклонения s(Е).

Случайная величина имеет нормальное распределение вероятностей с параметрами а и s,если плотность ее распределения задается формулой:

, .

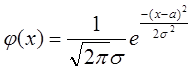
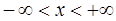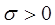Математическое ожидание и дисперсия нормальной случайной величины Е соответственно равны а и s²:

М(Е) = а VAR(E) = s²

Нормальное распределение обладает рядом важнейших свойств:

1. Вероятность больших отклонений нормальной случайной величины от центра ее распределения (параметра а) ничтожно мала;

2. График функции плотности нормального распределения симметричен относительно средней (параметра а);

3. Стандартное отклонениеs характеризует степень сжатия или растяжения графика функции плотности распределения вероятностей;

4. Нормальная случайная величина Е с математическим ожиданием а и стандартным отклонением s с вероятностью близкой к 1 попадает в интервал :

(а-3s)<=E<=(a+3s) (правило трех сигм)

Закон нормального распределения вероятностей широко используется в процессе анализа рисков финансовых операций. Его важнейшие свойства, такие как симметричность распределения относительно средней, ничтожно малая вероятность больших отклонений значений случайной величины от центра ее распределения, правило 3-х сигм, позволяет существенно упростить проведение анализа и проведение сопутствующих расчетов.

Вид нормального распределения представлен на Рисунок 1. Нормальное распределение.

Рисунок 1. Нормальное распределение

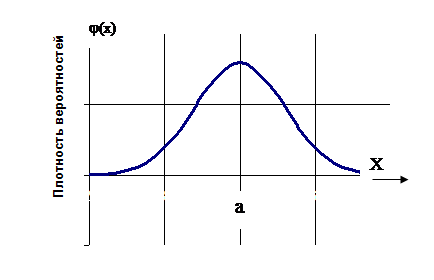Рисунок 2

Где а – математическое ожидание М(Е)