Коэффициент вариации

Еще одним полезным показателем является коэффициент вариации, исчисляемый по формуле:

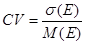
В отличие от стандартного отклонения коэффициент вариации – относительный показатель. В случае одинаковых или нулевых средних значений вычисление этого показателя теряет смысл. Очевидно, что при равных средних, чем больше величина стандартного отклонения s , тем больше коэффициент вариации. Помимо среднего значения и стандартного отклонения, асимметричные распределения часто требуют знания дополнительного параметра – коэффициента асимметрии (скоса).

Коэффициент асимметрии (скоса)

Коэффициент асимметрии (скоса) представляет собой нормированную величину и определяется по формуле:

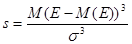
Коэффициент асимметрии может использоваться для приблизительной проверки гипотезы о нормальном распределении случайной величины. Его значение в этом случае должно быть равно 0.

Эксцесс

Некоторые симметричные распределения могут характеризоваться четвертым нормированным центральным моментом – эксцессом, вычисляемым по формуле:

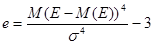
Если значение эксцесса больше нуля, кривая распределения более остроконечна, чем нормальная кривая. В случае отрицательного эксцесса кривая распределения более полога по сравнению с нормальной.