Среднее (ожидаемое) значение случайной величины

Концепция среднего широко используется практически во всех сферах человеческой деятельности. Средний возраст, средние объемы потребления, средняя заработная плата, средняя доходность – все это далеко не полный перечень показателей, ежедневно встречающихся в средствах массовой информации. Концепция среднего не только полезна, но и интуитивно понятна. Говоря о средних величинах, часто используют термин «ожидаемое значение».

Средним, или ожидаемым, значением (математическим ожиданием)дискретной величины Е называется сумма произведений ее значений на их вероятности:

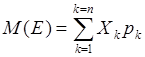
Выделяют следующие свойства этого показателя:

1) постоянный множитель С можно выносить за знак математического ожидания:

М(СЕ)=СМ(Е)

2) математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий:

M(E+G)= M(E)+M(G)

3) математическое ожидание постоянной величины С равно этой величине:

М(С) = С

4) математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий:

M(E*G) = M(E)*M(G)

В случае равной вероятности наступления каждого из событий математическое ожидание вычисляется как арифметическое среднее:

=

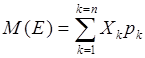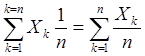
Математическое ожидание (среднее, или ожидаемое, значение) важнейшая характеристика случайной величины, так как служит центром распределения ее вероятностей.