Случайные величины и законы их распределений
Случайной называется величина, которая под воздействием случайных факторов может с определенными вероятностями принимать те или иные значения из некоторого множества чисел. Случайные величины можно разделить на два основных вида –дискретные и непрерывные. Величина Е называется дискретной случайной величиной, если множество ее возможных значений Х1, Х2 …….Хк конечно или счетно и принятие ею каждого из указанных значений есть случайное событие с определенной вероятностью.
Любое правило, позволяющее находить вероятности всех значений случайной величины Е, называют законом распределения ее вероятностей.Для дискретной случайной величины этот закон задается в виде таблицы, в которой перечисляют все ее возможные значения и их вероятности. При этом число ее значений конечно, сумма их вероятностей равна 1:
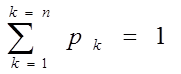
Задание закона распределения вероятностей в виде таблицы не совсем удобно, т.к. таблица может быть настолько большой, что станет непригодной или неудобной для практического применения.
Таблица 2
| Событие | Доходность акций в % | Вероятность |
| Подъем | 0,33 | |
| Без изменений | 0,33 | |
| Спад | 0,33 |
Поэтому для удобства проведения анализа, распределения случайных дискретных величин аппроксимируют непрерывными распределениями, позволяющими использовать сравнительно простые методы расчетов даже при неограниченном количестве сценариев. Для задания таких распределений используется функция F(X), называемая функцией распределения случайной величины.
Функцией F(X) распределения вероятностей случайной величины Еназывается вероятность того, что она примет значение, не превосходящее число х:
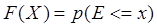
Если функция распределения F(X) непрерывна и дифференцируема, то ее производная F(X) называется плотностью распределения вероятностей. Тогда функцию распределения вероятностей можно определить как:
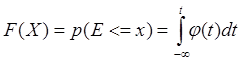
где F(X) изменяется на отрезке [0;1] j(t) – значение функции плотности вероятностей случайной величины Е.
Функция F(X) дает полную информацию о законе распределения случайной величины. Таким образом, зная функцию распределения либо плотность распределения вероятностей случайной величины, можно делать выводы о степени достоверности осуществления порождающих ее событий.
Дата добавления: 2019-04-03; просмотров: 347;
