Дисперсия и стандартное отклонение

Случайной величины

Дисперсия и стандартное отклонение служат характеристиками разброса (вариации) случайной величины от ее центра распределения (среднего значения М(Е)). Необходимость и полезность применения этих показателей хорошо иллюстрирует анекдот про математика, который свято верил в значимость средних величин и утонул в речке, средняя глубина которой не превышала половины его роста.

Дисперсиейназывается сумма квадратов отклонений случайной величины от ее среднего значения, взвешенных на соответствующие вероятности:

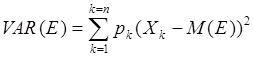
Отметим следующие свойства этого показателя:

1. Дисперсия постоянной величины равна 0

2. Для любой неслучайной постоянной С:

VAR(C+E) = VAR(E),

VAR(CE) = C²VAR(E)

Применение дисперсии не всегда удобно. Размерность дисперсии равна квадрату единицы измерения случайной величины.

На практике результаты анализа более наглядны, если показатель разброса случайной величины выражен в тех же единицах измерения, что и сама случайная величина. Для этих целей в качестве меры разброса случайной величины удобно использовать другой показатель – стандартное (среднее квадратическое) отклонение, рассчитываемое по формуле:

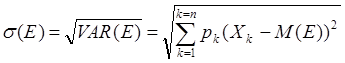
Отсюда следует, что величина s представляет собой средневзвешенное отклонение случайной величины от ее математического ожидания, при этом в качестве весов берутся соответствующие вероятности. Будучи выражено, в тех же единицах, стандартное отклонение показывает, насколько значения случайной величины могут отличаться от ее среднего.