Построение имитационной модели методом Монте-Карло

При вычислениях методом Монте-Карло статистические результаты получаются путем повторяющихся испытаний. Вероятность того, что эти результаты отличаются от истинных не более, чем на заданную величину, есть функция количества испытаний.

В основе вычислений по методу Монте-Карло лежит случайный выбор чисел из заданного вероятностного распределения. При практических вычислениях эти числа берут из таблиц или получают путем некоторых операций, результатами которых являются псевдослучайные числа с теми же свойствами, что и числа, получаемые путем случайной выборки. Имеется большое число вычислительных алгоритмов, которые позволяют получить данные последовательности псевдослучайных чисел.

Обозначим P{} теоретическое распределение, для которого мы хотим генерировать последовательность случайных чисел. Для любого отрезка [a,b] по определению P{[a,b]} равно вероятности того, что случайная величина, подчиняющаяся данному распределению, попадет в отрезок [a,b].

Пусть N количество чисел в последовательности, полученной с помощью датчика случайных чисел. Обозначим P_N{} соответствующее эмпирическое распределение. ( По определению, 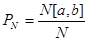, где N[a,b] количество чисел последовательности, попавших в отрезок [a,b].) Если последовательность случайных чисел распределена в соответствии с теоретическим распределением P{} , то для любого отрезка [a,b] при достаточно большом количестве N чисел в последовательности имеет место приблизительное равенство P_N{[a,b]}= P{[a,b]}. (В пределе должно выполняться строгое равенство lim P_N{[a,b]}= P{[a,b]}

N®¥

Покажем, каким образом, зная теоретические распределения входных параметров модели, можно построить эмпирическое распределение выходного параметра.

Пусть модель задана в виде Y=f (X₁, X₂,…. X_m). На основании известных теоретических распределений входных параметров X₁, X₂,…. X_m для каждого входного параметра X_k с помощью датчика случайных чисел строится последовательность чисел X_k1, X_k2,…. X_kN, подчиняющаяся соответствующему теоретическому распределению. Затем с помощью последовательностей X_k1, X_k2,…. X_kN , k=1,m ,строится последовательность чисел Y₁,Y₂, Y _N для выходного параметра Y по формуле Y_j=f(X_1j, X_2j,…. X_mj), где j=1,N.

Полученная последовательность Y₁,Y₂, Y _N естественным образом задает эмпирическое распределение выходного параметра Y.