Анализ коэффициентов и свободных членов канонических уравнений метода перемещений.

Все коэффициенты канонических и свободные члены канонических уравнений метода перемещений являются реактивными усилиями, возникающими в дополнительно введенных связях основной системы, от загружения её одним углом поворота, численно равным 1 (единице), одним линейным смещением, численно равным 1 (единице), или всеми заданными внешними силами одновременно.

Первый индекс коэффициента или свободного члена канонических уравнений соответствует порядковому номеру дополнительно введенной связи основной системы. Второй индекс соответствует номеру единичного перемещения (угла поворота или линейного перемещения) или всех внешних нагрузок, приложенных к основной системе. Физический смысл каждого коэффициента и свободного члена канонических уравнений совпадает с физическим смыслом этих уравнений. В плавающих заделках основной системы возникают реактивные моменты, а в шарнирно стержневых связях возникают сосредоточенные силы.

Например, коэффициент 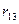- есть реактивное усилие, возникающее в дополнительно введенной связи 1 основной системы, загруженной кинематическим воздействием 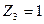(углом поворота узла 3 или его линейным смещением).

Свободные члены канонических уравнений являются реактивными усилиями в дополнительно введенных связях основной системы, загруженной заданными внешними нагрузками.

Например, 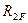- есть грузовое реактивное усилие в дополнительно введенной связи 2 основной системы, загруженной внешними заданными нагрузками.

Все коэффициенты канонических уравнений метода перемещений (как и в методе сил) разделяют на главные и побочные. Главные коэффициенты имеют одинаковые индексы, располагаются по главной диагонали системы канонических уравнений и всегда имеют положительные значения. Побочные коэффициенты имеют разные индексы и могут иметь положительные, отрицательные или нулевые значения. Побочные коэффициенты, расположенные симметрично главной диагонали имеют одинаковые численные значения, т.е. обладают свойством взаимности ( 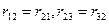и т.д.).