Проверка равновесия рамы в целом
Итоговой проверкой правильности построения эпюр внутренних усилий в статически неопределимой раме, является проверка равновесия системы в целом. Для её выполнения необходимо освободить заданную раму от всех опорных связей и загрузить её заданными нагрузками и реакциями освобожденных опор. Величины и направления реакций опор легко установить по эпюрам 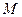 ,
, 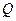 ,
, 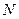 .
.
Загруженная, таким образом, рама должна удовлетворять трем условиям равновесия плоской системы сил:
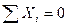 ,
, 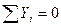 ,
, 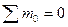 .
.
Если уравнения равновесия, составленные с использованием этих условий, тождественно удовлетворяются, то расчет заданной рамы выполнен без ошибок.
Пример 8.1 Построить эпюры изгибающих моментов, поперечных и продольных сил для рамы, представленной на рис.8.23.
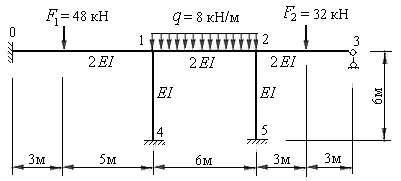
Рис.8.23
Последовательность решения задачи:
1) Устанавливаем степень кинематической неопределимости заданной рамы, используя формулу 1:
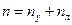
Число жестких узлов для заданной рамы равно 2, а число линейных смещений равно нулю, так как узлы 1 и 2 заданной рамы не могут иметь линейных смещений ни в горизонтальном направлении (этому препятствует защемленная опора 0), ни в вертикальном направлении (этому препятствуют защемленные опоры 4 и 5).
Можно образовать условную шарнирную схему заданной рамы и определить число 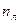 по формуле 8.2 § 8.1. Оно будет равным нулю (см. условную шарнирную схему рамы 3, приведенную в § 8.1).
по формуле 8.2 § 8.1. Оно будет равным нулю (см. условную шарнирную схему рамы 3, приведенную в § 8.1).
Таким образом, заданная рама имеет две неизвестные метода перемещений: 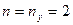 .
.
2) Образуем основную систему метода перемещений. Для этого в жесткие узлы 1 и 2 заданной рамы вводим плавающие заделки. В результате основная система будет состоять из четырех стержней, имеющих две защемленные опоры, и одного стержня, имеющего одну защемленную и другую шарнирную опоры. На рис.8.24 показана основная система метода перемещений, образованной для заданной рамы. В отличие от основной системы метода сил, основная система метода перемещений имеет единственный вариант.
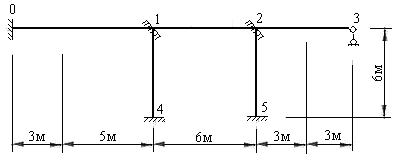
Рис.8.24
Вычисляем погонные жесткости стержней рамы и приводим их к одной минимальной жесткости 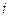 :
: 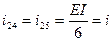 ,
,
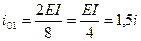 ,
, 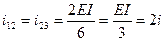
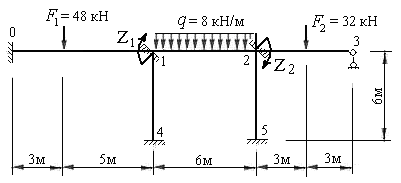
Рис.8.25
3) Образуем эквивалентную систему метода перемещений путем загружения основной системы заданными нагрузками и неизвестными углами поворота жестких узлов 1 и 2. На рис.8.25 показана эквивалентная система.
4) Записываем систему канонических уравнений метода перемещений:
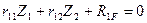
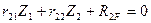
Первое каноническое уравнение отрицает наличие реактивного момента в плавающей заделке 1 эквивалентной системы, следовательно, коэффициенты 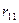 ,
, 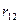 и грузовая реакция
и грузовая реакция 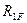 являются реактивными моментами в плавающей заделке 1 основной системы, загруженной соответственно единичными поворотами жестких узлов в отдельности и всеми заданными нагрузками.
являются реактивными моментами в плавающей заделке 1 основной системы, загруженной соответственно единичными поворотами жестких узлов в отдельности и всеми заданными нагрузками.
Второе каноническое уравнение имеет такой же физический смысл, следовательно, коэффициенты 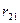 ,
, 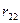 и грузовая реакция
и грузовая реакция 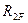 являются реактивными моментами в плавающей заделке 2 основной системы, загруженной соответственно единичными поворотами жестких узлов в отдельности и всеми заданными нагрузками.
являются реактивными моментами в плавающей заделке 2 основной системы, загруженной соответственно единичными поворотами жестких узлов в отдельности и всеми заданными нагрузками.
Это важно знать для выбора рационального метода вычисления коэффициентов и грузовых реакций канонических уравнений.
5) Строим единичные и грузовую эпюры изгибающих моментов в основной системе:
- Загружаем основную систему метода перемещений единичным углом поворота жесткого узла 1, который содержит плавающую заделку. Используя эпюру п. 1 § 8.6 (с учетом вычисленных погонных жесткостей каждого стержня) строим единичную эпюру 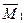 (рис.8.26) для каждого из трех стержней, объединенных в узле 1.
(рис.8.26) для каждого из трех стержней, объединенных в узле 1.
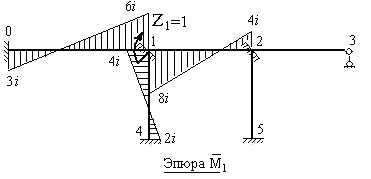
Рис.8.26
- Загружаем основную систему метода перемещений единичным углом поворота жесткого узла 2, который содержит плавающую заделку. Используя эпюры п. 1 и п. 3 § 8.6, с учетом вычисленных погонных жесткостей каждого стержня, строим единичную эпюру 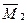 (рис.8.27).
(рис.8.27).
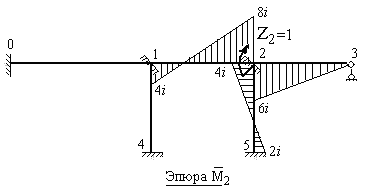
Рис.8.27
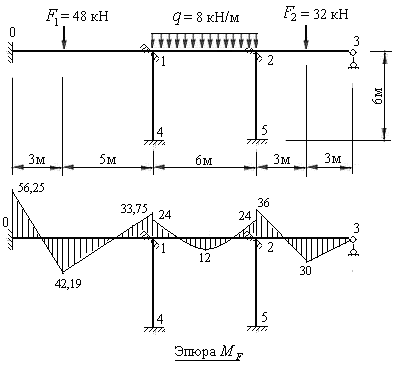
Рис.8.28
- Загружаем основную систему метода перемещений заданными нагрузками. Используя эпюру п. 5 § 8.6 для стержня 1-2, п. 6 § 8.6 при значениях 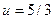 и
и 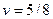 для стержня 0-1 и частный случай п. 8 § 8.6 для стержня 2-3, строим грузовую эпюру
для стержня 0-1 и частный случай п. 8 § 8.6 для стержня 2-3, строим грузовую эпюру 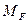 (рис.8.28).
(рис.8.28).
6) Определяем коэффициенты и грузовые реакции канонических уравнений метода перемещений.
Вырезаем узел 1 из единичных и грузовой эпюр изгибающих моментов и загружаем его неизвестными реактивными моментами в плавающей заделке 1, а также узловыми моментами в рассеченных стержнях рамы. Величины и направления указанных моментов устанавливаем по эпюрам изгибающих моментов.
На рис.8.29 изображен узел 1, вырезанный из трех эпюр и показаны все действующие на него моменты. Используя условие равновесия 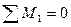 , составляем уравнения равновесия и определяем коэффициенты и грузовую реакцию первого канонического уравнения.
, составляем уравнения равновесия и определяем коэффициенты и грузовую реакцию первого канонического уравнения.
Узел 1, вырезанный Узел 1, вырезанный Узел 1, вырезанный
из эпюры 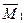 из эпюры
из эпюры 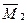 из эпюры
из эпюры 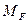
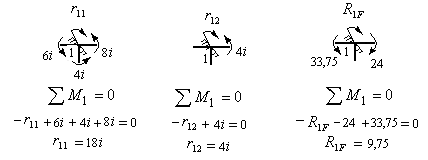
Рис.8.29
Вырезаем узел 2 из единичных и грузовой эпюр изгибающих моментов и загружаем его неизвестными реактивными моментами в плавающей заделке 2, а также узловыми моментами в рассеченных стержнях рамы. Величины и направления указанных моментов устанавливаем по эпюрам изгибающих моментов.
На рис.8.30 изображен узел 2, вырезанный из трех эпюр и показаны все действующие на него моменты. Используя условие равновесия 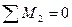 , определяем коэффициенты и грузовую реакцию первого канонического уравнения.
, определяем коэффициенты и грузовую реакцию первого канонического уравнения.
Узел 2, вырезанный Узел 2, вырезанный Узел 2, вырезанный
из эпюры 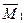 из эпюры
из эпюры 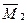 из эпюры
из эпюры 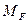
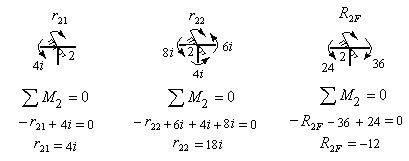
Рис.8.30
7) Подставляем значения коэффициентов и грузовых реакций в канонические уравнения, получим следующую систему линейных алгебраических уравнений:
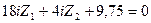
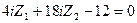
Из решения этой системы уравнений методом определителей или методом последовательного исключения неизвестных, получаем:
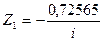 ,
, 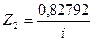
8) Строим исправленные эпюры изгибающих моментов в основной системе. Для этого умножаем ординаты единичных эпюр изгибающих моментов на соответствующие величины углов поворота жестких узлов рамы. На рис.34 и 35 приведены исправленные эпюры 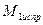 и
и 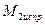 .
.
На исправленных эпюрах изгибающих моментов ординаты выражены в кН∙м. На этих же эпюрах вычислены и показаны ординаты изгибающих моментов под точками приложения сосредоточенных сил и по середине пролета 1-2, загруженного распределенной нагрузкой.
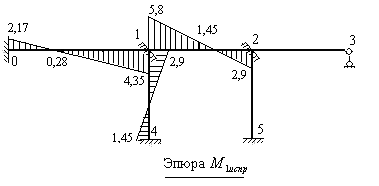
Рис.8.31
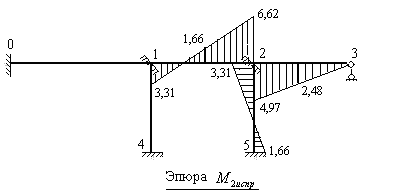
Рис.8.32
9). Строим эпюру изгибающих моментов в заданной статически неопределимой раме. Для этого суммируем алгебраически в каждом характерном сечении рамы ординаты грузовой эпюры изгибающих моментов с ординатами двух исправленных эпюр изгибающих моментов, построенных в основной системе метода перемещений. В незагруженных стержнях рамы достаточно вычислить ординаты в двух сечениях (узловом и опорном). В загруженных стержнях следует определять как минимум три ординаты (в узловом и опорном сечениях и под сосредоточенной силой или по середине пролета, загруженного распределенной нагрузкой).
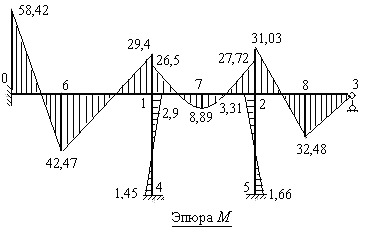
Рис.8.33
На рис.8.33 построена эпюра изгибающих моментов в заданной статически неопределимой раме.
10) Проверяем построенную эпюру М.
10.1 Статическая проверка. Вырезаем жесткие узлы 1 и 2 заданной рамы и загружаем их узловыми изгибающими моментами. Величины и направления этих моментов устанавливаем по эпюре М (рис.8.34).
Узел 1, вырезанный Узел 2, вырезанный
из эпюры М из эпюры М
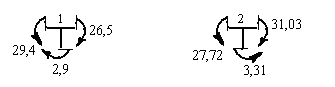
Рис.8.34
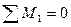
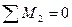
29,4-26,5-2,9=0 27,72+3,31-31,03=0
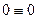
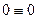
Таким образом, статическая проверка эпюры изгибающих моментов в заданной раме выполняется. Напомним, что в методе перемещений статическая проверка, если она выполняется, является надежным подтверждением того, что эпюра изгибающих моментов построена правильно.
10.2 Деформационная проверка.
Устанавливаем число неизвестных метода сил для заданной рамы. Поскольку рама состоит из одного диска, закрепленного десятью опорными связями, то по методу сил она имеет 7 лишних связей.
Образуем один из вариантов основной системы путем освобождения всех связей в опорах 0, 3 и 4. Основная система метода сил показана на рис.8.35.
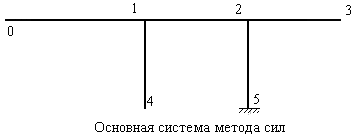
Рис.8.35
Загрузим её единичной реакцией одной из удаленных опорных связей, например 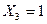 , и построим единичную эпюру
, и построим единичную эпюру 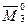 (рис.8.36).
(рис.8.36).
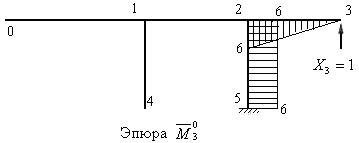
Рис.8.36
Перемножаем по правилу Верещагина эпюру М в заданной раме на единичную эпюру 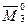 . Перемножение осуществляем на двух участках 2-3 и 2-5. При этом эпюру М на участке 2-3 расчленяем на два треугольника, основанием которых является длина стержня 2-3. Тогда высота треугольника, расположенного ниже оси стержня будет равна 32,48+31,03/2= 48 (кН∙м), а высота треугольника, расположенного выше оси стержня будет равна 31,03 (кН∙м). Площади и положения центров тяжести этих треугольников легко определяются. Ординаты единичной эпюры под центрами тяжести указанных треугольников так же легко вычисляются. На участке 2-5 обе эпюры изгибающих моментов прямолинейные, поэтому порядок их перемножения можно изменить.
. Перемножение осуществляем на двух участках 2-3 и 2-5. При этом эпюру М на участке 2-3 расчленяем на два треугольника, основанием которых является длина стержня 2-3. Тогда высота треугольника, расположенного ниже оси стержня будет равна 32,48+31,03/2= 48 (кН∙м), а высота треугольника, расположенного выше оси стержня будет равна 31,03 (кН∙м). Площади и положения центров тяжести этих треугольников легко определяются. Ординаты единичной эпюры под центрами тяжести указанных треугольников так же легко вычисляются. На участке 2-5 обе эпюры изгибающих моментов прямолинейные, поэтому порядок их перемножения можно изменить.
Результат перемножения эпюр М и 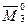 определяет вертикальное перемещение опоры 3 в заданной раме и должен быть равным нулю, так как опора 3 заданной рамы исключает вертикальное перемещение.
определяет вертикальное перемещение опоры 3 в заданной раме и должен быть равным нулю, так как опора 3 заданной рамы исключает вертикальное перемещение.
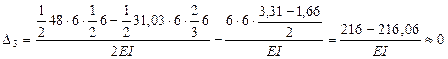
Таким образом, деформационная проверка эпюры М выполняется.
11) Определяем поперечные силы и строим эпюру 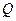 .
.
Рассматриваем сначала все участки, на которых эпюра изгибающих моментов ограничена прямой линией и вычисляем поперечные силы по формуле (8.11):
Участок 0-6 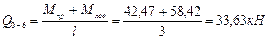
Участок 6-1 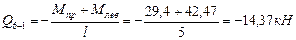
Участок 2-8 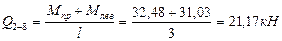
Участок 8-3 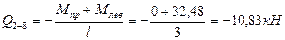
Участок 1-4 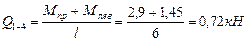
Участок 2-5 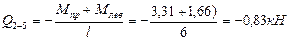
На участке 1-2 заданной рамы эпюра изгибающих моментов имеет криволинейное очертание, поэтому поперечные силы определяем по формулам (8.12) и (8.13):
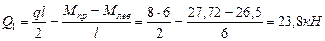
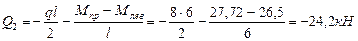
Строим эпюру поперечных сил. Ординаты поперечных сил, имеющих знак плюс, откладываем вверх от осей горизонтальных стержней и влево от осей вертикальных стержней. Ординаты поперечных сил, имеющих знак минус, откладываем вниз от осей горизонтальных стержней и вправо от осей вертикальных стержней. На рис.8.36 построена эпюра Q.
12) Определяем продольные силы в стержнях заданной рамы и строим эпюру N
Анализируя заданную раму легко установить, что продольная сила в
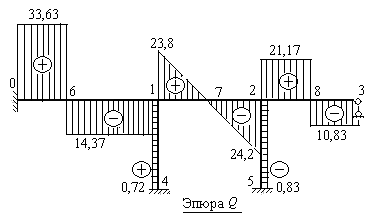
Рис.8.36
стержне 2-3 равна нулю, так как этот стержень не является опорным в направлении своей оси. Следовательно, для определения продольных сил, необходимо рассмотреть сначала равновесие узла 2, а затем равновесие узла 1.
Вырезаем узел 2 заданной рамы и загружаем его неизвестными продольными силами, возникающими в стержнях 2-1 и 2-5, а также поперечными силами, действующими в узловых сечениях трех рассеченных стержней. Величины и направления этих сил определяем по эпюре Q. Поперечную силу, имеющую знак плюс, направляем так, чтобы она вращала узел по часовой стрелке. Поперечная сила, имеющая знак минус должна вращать узел против часовой стрелки. На рис.8.37 показаны все силы, действующие на узел 2.
Составляем два уравнения равновесия этого узла и вычисляем продольные силы в стержнях 2-1 и 2-5.
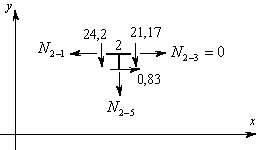
Рис.8.37
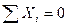

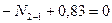

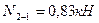
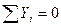

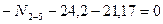

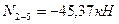
Вырезаем узел 1 заданной рамы. Этот узел загружаем неизвестными продольными силами, возникающими в стержнях 1-0 и 1-4, известной продольной силой в стержне 1-2, а также поперечными силами, действующими в узловых сечениях трех рассеченных стержней. Величины и направления этих сил определяем по эпюре Q. На рис.8.38 показаны все силы, действующие на узел 1.
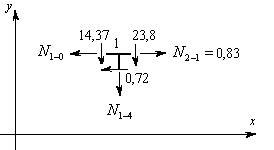
Рис.8.38
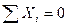

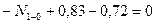

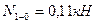
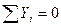

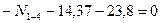

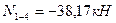
Эпюра продольных сил построена на рис.8.39.
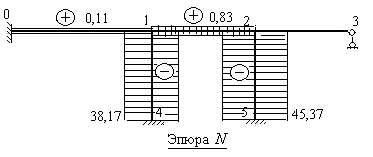
Рис.8.39
13) Проверяем равновесие заданной рамы в целом.
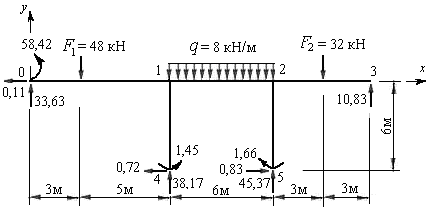
Рис.8.40
Освобождаем раму от всех опорных связей и загружаем её заданными нагрузками и реакциями освобожденных связей. Величины и направления этих реакций устанавливаем по эпюрам изгибающих моментов (реактивные моменты в защемленных опорах рамы), поперечных и продольных сил (вертикальные и горизонтальные реакции в опорах). На рис 8.40 показаны все нагрузки и реакции опор, действующие на раму.
Составляем три уравнения равновесия и убеждаемся, что они тождественно удовлетворяются.
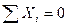

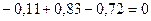

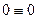
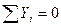

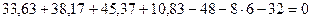

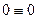
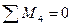

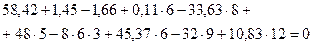
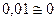
Пример 8.2. Построить эпюры изгибающих моментов, поперечных и продольных сил для рамы, представленной на рис.8.41. Размеры и нагрузки показаны на расчетной схеме рамы. Жесткости стоек принять равными EI, жесткость левого ригеля принять равным 3EI , а жесткость правого ригеля принять равным 2,25EI .
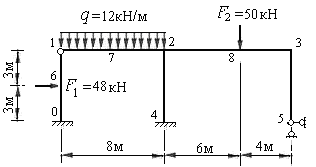
Рис.8.41
Последовательность расчета рамы методом перемещений:
1) Устанавливаем степень кинематической неопределимости заданной рамы по формуле 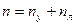 ,
, 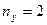 (число жестких узлов заданной рамы),
(число жестких узлов заданной рамы), 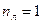 (число линейных смещений узлов рамы). Из анализа заданной рамы следует, что её узлы могут перемещаться в горизонтальном направлении на величину, допускаемую связями рамы и определяемую из решения канонических уравнений метода перемещений.
(число линейных смещений узлов рамы). Из анализа заданной рамы следует, что её узлы могут перемещаться в горизонтальном направлении на величину, допускаемую связями рамы и определяемую из решения канонических уравнений метода перемещений.
Если из анализа заданной рамы не удается установить число и направления линейных смещений узлов, то следует образовать условную шарнирную схему и определить степень её геометрической изменяемости по формуле (8.2).
2) Образуем основную систему метода перемещений. Для этого вводим в шарнирный узел 1 шарнирно стержневую связь на горизонтальное перемещение и плавающие заделки в жесткие узлы 2 и 3 (рис.8.42).
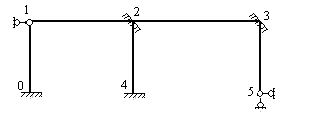
Рис.8.42
Определяем погонные жесткости стержней рамы:
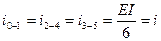 ,
, 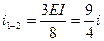 ,
, 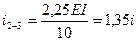
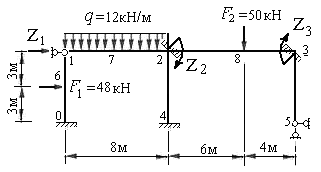
Рис.8.43
3) Образуем эквивалентную систему метода перемещений путем загружения основной системы заданными нагрузками и неизвестными углами поворота жестких узлов 2 и 3, а также линейным горизонтальным смещением всех узлов на одинаковую величину. На рис.8.43 показана эквивалентная система. Для этой системы должны выполняться три условия эквивалентности: 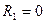 ,
, 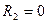 ,
, 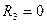 , где:
, где: 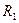 - горизонтальная реакция в шарнирно стержневой связи 1;
- горизонтальная реакция в шарнирно стержневой связи 1;
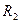 - реактивный момент в плавающей заделке 2;
- реактивный момент в плавающей заделке 2;
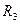 - реактивный момент в плавающей заделке 3.
- реактивный момент в плавающей заделке 3.
4) Записываем систему трех канонических уравнений метода перемещений:
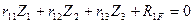
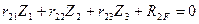
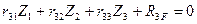
Первое каноническое уравнение отрицает наличие горизонтальной реакции в дополнительно введенной шарнирно стержневой связи эквивалентной системы, следовательно, все коэффициенты и грузовая реакция являются сосредоточенными горизонтальными силами, возникающими в указанной шарнирно стержневой связи основной системы, загруженной соответственно линейным смещением 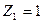 , углами поворота
, углами поворота 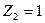 и
и 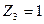 , а также заданными внешними нагрузками.
, а также заданными внешними нагрузками.
Второе и третье канонические уравнения отрицают наличие реактивных моментов в дополнительно введенных плавающих заделках эквивалентной системы, следовательно, все коэффициенты и грузовые реакции этих уравнений являются реактивными моментами, возникающими в плавающих заделках 2 и 3 основной системы, загруженной соответственно линейным смещением 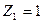 , углами поворота
, углами поворота 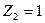 и
и 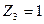 , а также заданными внешними нагрузками.
, а также заданными внешними нагрузками.
Анализ физической сущности канонических уравнений, их коэффициентов и грузовых реакций, дает возможность выбрать рациональный метод вычисления этих усилий.
5) Строим единичные и грузовую эпюры изгибающих моментов в основной системе:
- Загружаем основную систему единичным линейным смещением 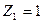 и строим единичную эпюру
и строим единичную эпюру 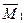 , используя формулы п. 2 § 8.6 для стойки 2-4 и п. 4 § 8.6 для стоек
, используя формулы п. 2 § 8.6 для стойки 2-4 и п. 4 § 8.6 для стоек
0-1 и 3-5 (рис.8.44).
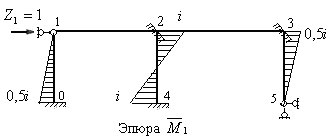
Рис.8.44
- Загружаем основную систему единичным углом поворота 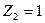 плавающей заделки 2 и строим единичную эпюру
плавающей заделки 2 и строим единичную эпюру 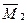 , используя формулы п. 1 § 8.6 для стержней 2-4 и 2-3 и п. 3 § 8.6 для стержня 1-2 (рис.8.45).
, используя формулы п. 1 § 8.6 для стержней 2-4 и 2-3 и п. 3 § 8.6 для стержня 1-2 (рис.8.45).
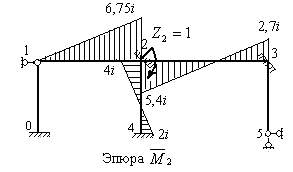
Рис.8.45
- Загружаем основную систему единичным углом поворота 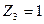 плавающей заделки 3 и строим единичную эпюру
плавающей заделки 3 и строим единичную эпюру 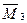 , используя формулы п. 1 § 8.6 для стержня 2-3 и формулы п.3 § 8.6 для стержня 3-5 (рис.8.46).
, используя формулы п. 1 § 8.6 для стержня 2-3 и формулы п.3 § 8.6 для стержня 3-5 (рис.8.46).
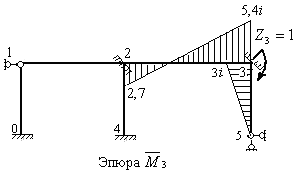
Рис.8.46
- Загружаем основную систему заданными нагрузками и строим грузовую эпюру изгибающих моментов 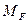 , используя формулы п. 6 § 8.6 для стержня 1-2, формулы п.7 § 8.6 для стержня 2-3 и формулы п. 8 § 8.6 (частный случай) для стержня 0-1 (рис.8.47).
, используя формулы п. 6 § 8.6 для стержня 1-2, формулы п.7 § 8.6 для стержня 2-3 и формулы п. 8 § 8.6 (частный случай) для стержня 0-1 (рис.8.47).
Рис.8.47
6) Определяем коэффициенты и грузовые реакции канонических уравнений статическим методом равновесия дисков или узлов, в зависимости от того, являются ли определяемые неизвестные сосредоточенными силами или сосредоточенными моментами.
Ранее было установлено, что коэффициенты и грузовая реакция первого канонического уравнения являются сосредоточенными силами, возникающими в шарнирно стержневой связи 1 основной системы, загруженной последовательно единичными смещением и углами поворота узлов 2 и 3, а также заданными внешними нагрузками.
Для их определения вырезаем круговым замкнутым сечением диск 1-2-3 из всех единичных и грузовой эпюр изгибающих моментов. Этот диск загружаем неизвестной реактивной силой и известными поперечными силами в сечениях стоек.
Величины и знаки поперечных сил определяем по формуле Журавского. Поперечные силы, имеющие знак плюс, направляем так, чтобы они вращали вырезанный диск по ходу часовой стрелки, а поперечные силы, имеющие знак минус, направляем так, чтобы они вращали диск против движения часовой стрелки.
На рис.8.48 показан диск 1-2-3, вырезанный из всех четырех эпюр изгибающих моментов, построенных в п.5), и показаны все действующие на него силы. Используя условие равновесия 
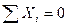 , составляем уравнения равновесия и вычисляем искомые коэффициенты и грузовую реакцию первого канонического уравнения.
, составляем уравнения равновесия и вычисляем искомые коэффициенты и грузовую реакцию первого канонического уравнения.
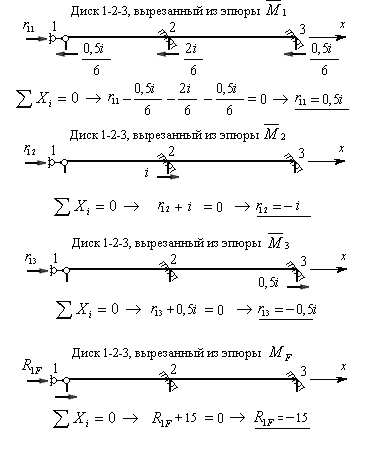
Рис.8.48
Коэффициенты и грузовая реакция второго и третьего канонических уравнений являются сосредоточенными реактивными моментами, возникающими в плавающих заделках 2 и 3 основной системы, загруженной последовательно единичным смещением и углами поворота узлов 2 и 3, а также заданными внешними нагрузками.
Для их определения вырезаем последовательно узел 2, а затем узел 3 из всех четырех эпюр изгибающих моментов, построенных в основной системе. Загружаем их, как показано на рис.8.49 и 8.50, составляем уравнения равновесия и вычисляем неизвестные коэффициенты и грузовые реакции второго и третьего канонических уравнений.
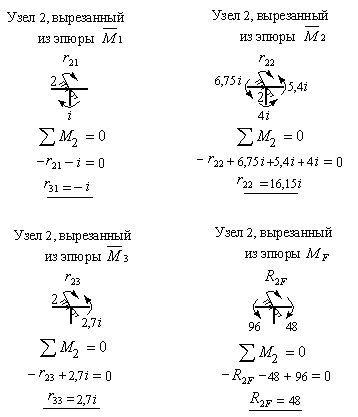
Рис.8.49
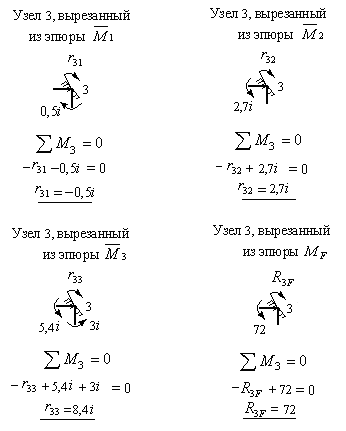
Рис.8.50
Вычислим коэффициенты первого канонического уравнения перемножением единичных эпюр изгибающих моментов по правилу Верещагина:
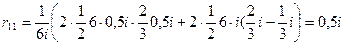
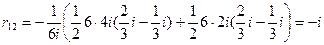
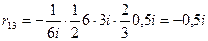
Сравнивая их с величинами, вычисленными статическим методом, убеждаемся, что они полностью совпадают.
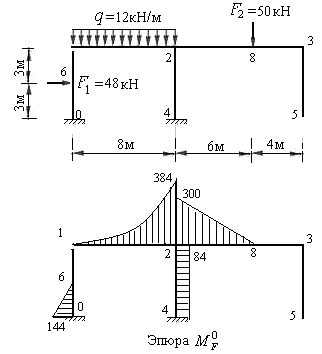
Рис.8.51
Для вычисления грузовой реакции 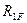 по правилу Верещагина построим дополнительно грузовую эпюру изгибающих моментов
по правилу Верещагина построим дополнительно грузовую эпюру изгибающих моментов 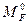 в основной системе метода сил (рис.8.51) и перемножим её на единичную эпюру
в основной системе метода сил (рис.8.51) и перемножим её на единичную эпюру 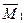 . Результат перемножения, взятый со знаком минус, будет равен искомой грузовой реакции, т.е.
. Результат перемножения, взятый со знаком минус, будет равен искомой грузовой реакции, т.е.
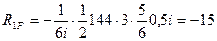
7) Подставляем вычисленные значения коэффициентов и грузовых реакций в канонические уравнения. Переносим, свободные члены уравнений в правые их части, получаем следующую систему трех уравнений с тремя неизвестными:
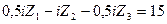
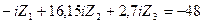
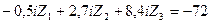
Из решения этой системы методом определителей с использованием функции МОПРЕД программы «Microsoft Excel»находим:
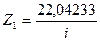 ,
, 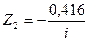 ,
, 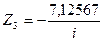
Подставляем эти значения в исходные уравнения, убеждаемся, что они тождественно удовлетворяется.
8) Строим исправленные эпюры в основной системе. Для этого ординаты единичных эпюр умножаем на вычисленные значения линейного смещения и углов поворота жестких узлов. На рис.56, 57 и 58 приведены исправленные эпюры 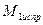 ,и
,и 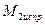 и
и 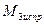 .
.
На исправленных эпюрах изгибающих моментов ординаты выражены в кН∙м. На этих же эпюрах вычислены и показаны ординаты изгибающих моментов под точками приложения сосредоточенных сил и по середине пролета 1-2, загруженного распределенной нагрузкой. Эти ординаты необходимы для определения изгибающих моментов в соответствующих сечениях заданной рамы.
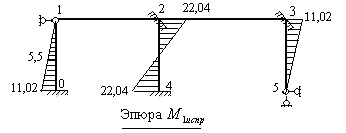
Рис.8.52
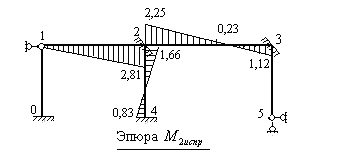
Рис.8.53
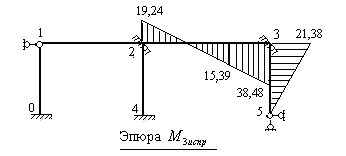
Рис.8.54
9) Вычисляем изгибающие моменты в характерных сечениях заданной рамы. К ним относятся: опорные и узловые сечения каждого стержня, а также сечения, под сосредоточенными силами и по середине пролета стержня, загруженного распределенной нагрузкой. Алгебраическая сумма ординат четырех эпюр (грузовой эпюры и всех исправленных эпюр) равна изгибающему моменту в рассматриваемом сечении заданной статически неопределимой рамы. На рис.8.55 построена эпюра 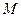 .
.
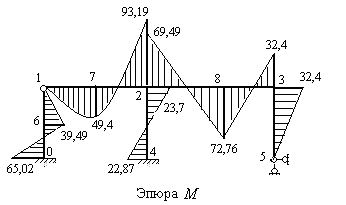
Рис.8.55
10) Выполняем статическую проверку эпюры 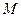 .
.
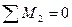

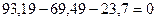

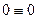
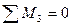

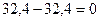

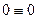
11) Вычисляем поперечные силы на отдельных участках заданной рамы по формуле Журавского и строим эпюру 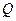 .
.
Участок 0-6 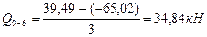
Участок 6-1 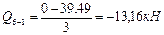
Участок 4-2 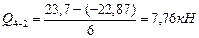
Участок 2-8 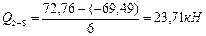
Участок 8-3 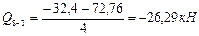
Участок 5-3 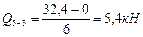
Участок 1-2 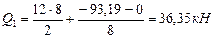
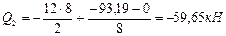
Строим эпюру поперечных сил 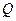 (рис.8.56)
(рис.8.56)
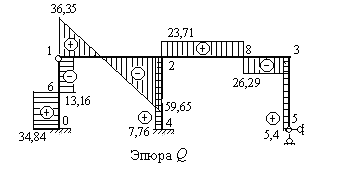
Рис.8.56
12) Вычисляем продольные силы в стержнях заданной рамы и строим эпюру 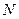 :
:
Вырезаем узел 1 заданной рамы. Этот узел загружаем неизвестными продольными силами, возникающими в стержнях 1-2 и 1-0, а также поперечными силами, действующими в узловых сечениях двух рассеченных стержней. Величины и направления этих сил определяем по эпюре Q. На рис.8.57 показаны все силы, действующие на узел 1.
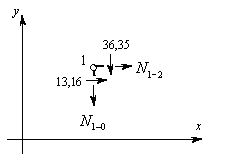
Рис.8.57
Составляем два уравнения равновесия этого узла и вычисляем продольные силы в стержнях 1-2 и 1-0.
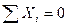

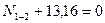

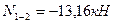
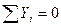

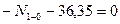

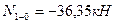
Вырезаем узел 2 заданной рамы. Этот узел загружаем неизвестными продольными силами, возникающими в стержнях 2-3 и 2-5, известной продольной силой в стержне 1-2, а также поперечными силами, действующими в узловых сечениях трех рассеченных стержней. Величины и направления этих сил определяем по эпюре Q. На рис.8.58 показаны все силы, действующие на узел 2.
Составляем два уравнения равновесия этого узла и вычисляем продольные силы в стержнях 2-3 и 2-4.
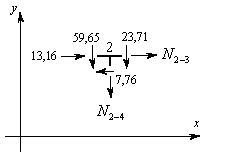
Рис.8.58
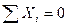

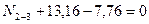

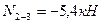
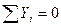

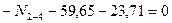

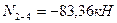
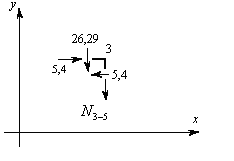
Рис.8.59
Вырезаем узел 3 заданной рамы. Этот узел загружаем неизвестной продольной силой, возникающей в стержне 3-5, известной продольной силой в стержне 2-3, а также поперечными силами, действующими в узловых сечениях двух рассеченных стержней. Величины и направления этих сил определяем по эпюре Q. На рис.8.59 показаны все силы, действующие на узел 3.
Составляем два уравнения равновесия этого узла. Одно уравнение равновесия должно тождественно удовлетворяться, и является проверочным, а из второго уравнения равновесия вычисляем продольную силу в стержне 3-6
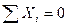

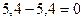

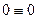
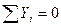

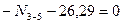

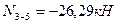
По вычисленным величинам продольных сил строим эпюру 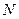 (рис.8.60).
(рис.8.60).
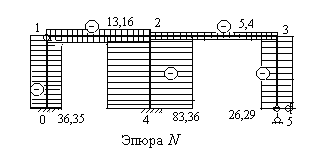
Рис.8.60
13) Проверяем равновесие рамы в целом. На рис.8.61 представлена рама без опорных связей. Она загружена заданными нагрузками и реакциями освобожденных опорных связей. Величины и направления указанных реакций устанавливаются по эпюрам 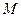 ,
, 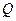 и
и 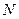 .
.
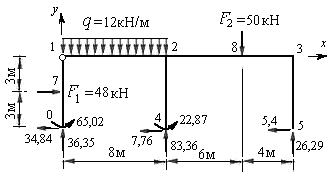
Рис.8.61
Составляем три уравнения равновесия и убеждаемся, что они тождественно удовлетворяются. Это является признаком правильного расчета заданной рамы.
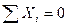

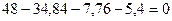

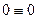
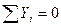

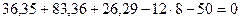

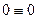
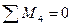

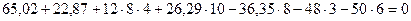

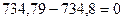

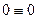
Пример 8.3. Построить эпюры изгибающих моментов, поперечных и продольных сил для однопролетной двухэтажной рамы, представленной на рис.8.62. Размеры и нагрузки показаны на расчетной схеме рамы. Жесткости всех стоек принять равными EI, а жесткости ригелей равными 2EI.
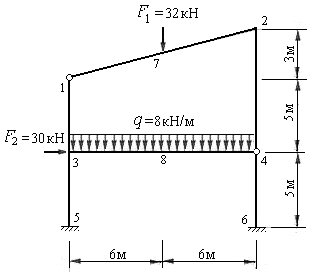
Рис.8.62
Последовательность расчета рамы методом перемещений:
1) Устанавливаем степень кинематической неопределимости заданной рамы по формуле 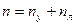 ,
, 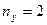 (число жестких узлов заданной рамы),
(число жестких узлов заданной рамы), 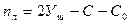 (число линейных смещений узлов рамы).
(число линейных смещений узлов рамы).
Образуем условную шарнирную схему заданной рамы путем введения полных цилиндрических шарниров в её жесткие узлы и защемленные опоры (рис.8.63).
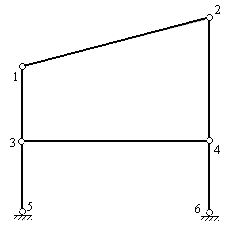
Рис.8.63
Для этой схемы имеем: 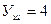 ,
, 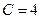 ,
, 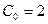 . Тогда
. Тогда  .
.
Таким образом, 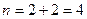 и заданная рама имеет четыре неизвестных метода перемещений (четыре раза кинематически неопределима).
и заданная рама имеет четыре неизвестных метода перемещений (четыре раза кинематически неопределима).
2) Образуем основную систему метода перемещений. Для этого вводим в шарнирные узлы 1 и 4 шарнирно стержневые связи на горизонтальное перемещение и в жесткие узлы 2 и 3 вводим плавающие заделки (рис.8.64).
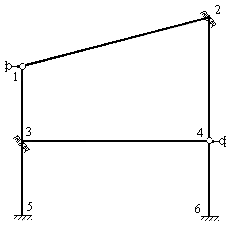
Рис.8.64
Определяем погонные жесткости стержней рамы:
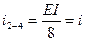 ,
, 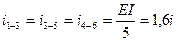 ,
,
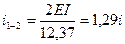 ,
, 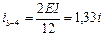
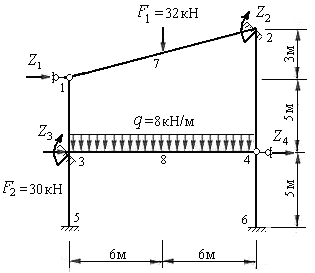
Рис.8.65
3) Образуем эквивалентную систему метода перемещений путем загружения основной системы заданными нагрузками и неизвестными углами поворота жестких узлов 2 и 3, а также линейными горизонтальными смещениями связей 1 и 4. На рис.8.65 показана эквивалентная система. Для этой системы должны выполняться четыре условия эквивалентности: 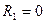 ,
, 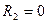 ,
, 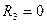 ,
, 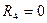 , где:
, где:
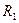 - горизонтальная реакция в шарнирно стержневой связи 1;
- горизонтальная реакция в шарнирно стержневой связи 1;
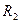 - реактивный момент в плавающей заделке 2;
- реактивный момент в плавающей заделке 2;
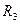 - реактивный момент в плавающей заделке 3.
- реактивный момент в плавающей заделке 3.
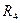 - горизонтальная реакция в шарнирно стержневой связи 4.
- горизонтальная реакция в шарнирно стержневой связи 4.
4) Записываем систему четырех канонических уравнений метода перемещений:
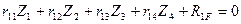
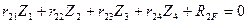
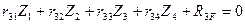
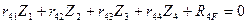
Первое и четвертое канонические уравнения отрицают наличие горизонтальных реакций в дополнительно введенных шарнирно стержневых связях эквивалентной системы, следовательно, все коэффициенты и грузовые реакции этих двух уравнений являются сосредоточенными горизонтальными силами, возникающими в указанных шарнирно стержневых связях основной системы, загруженной линейными смещениями 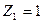 и
и 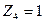 , углами поворота
, углами поворота 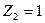 и
и 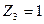 , а также заданными внешними нагрузками.
, а также заданными внешними нагрузками.
Второе и третье канонические уравнения отрицают наличие реактивных моментов в дополнительно введенных плавающих заделках эквивалентной системы, следовательно, все коэффициенты и грузовые реакции этих уравнений являются реактивными моментами, возникающими в плавающих заделках 2 и 3 основной системы, загруженной линейными смещениями 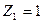 и
и 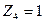 , углами поворота
, углами поворота 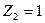 и
и 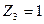 , а также заданными внешними нагрузками.
, а также заданными внешними нагрузками.
Напомним, что анализ физической сущности канонических уравнений, их коэффициентов и грузовых реакций, дает возможность выбрать рациональный метод вычисления этих усилий.
5) Строим единичные и грузовую эпюры изгибающих моментов в основной системе:
- Загружаем основную систему единичным линейным смещением 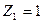 шарнирно стержневой связи 1 и строим единичную эпюру
шарнирно стержневой связи 1 и строим единичную эпюру 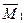 , используя формулы п. 4 § 8.6 для стоек 1-3 и 2-4 (рис.8.66).
, используя формулы п. 4 § 8.6 для стоек 1-3 и 2-4 (рис.8.66).
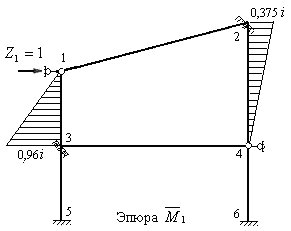
Рис.8.66
- Загружаем основную систему единичным углом поворота 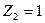 плавающей заделки 2 и строим единичную эпюру
плавающей заделки 2 и строим единичную эпюру 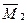 , используя формулы п.3 § 8.6 для стержней 1-2 и 2-4 (рис.8.67).
, используя формулы п.3 § 8.6 для стержней 1-2 и 2-4 (рис.8.67).
- Загружаем основную систему единичным углом поворота 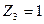 плавающей заделки 3 и строим единичную эпюру
плавающей заделки 3 и строим единичную эпюру 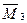 , используя формулы п. 1 § 8.6 для стержня 1-5 и формулы п.3 § 8.6 для стержней 3-1 и 3-4 (рис.8.68).
, используя формулы п. 1 § 8.6 для стержня 1-5 и формулы п.3 § 8.6 для стержней 3-1 и 3-4 (рис.8.68).
- Загружаем основную систему единичным линейным смещением 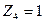 шарнирно стержневой связи 4 и строим единичную эпюру
шарнирно стержневой связи 4 и строим единичную эпюру 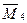 , используя формулы п. 2 § 8.6 для стержня 3-5 и формулы п.3 § 8.6 для стержней 3-1 и 4-2 и 4-6 (рис.8.69)
, используя формулы п. 2 § 8.6 для стержня 3-5 и формулы п.3 § 8.6 для стержней 3-1 и 4-2 и 4-6 (рис.8.69)
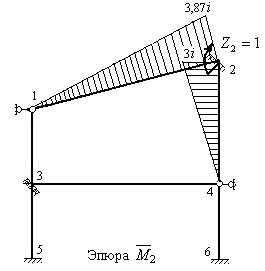
Рис.8.67
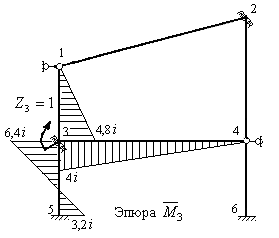
Рис.8.68
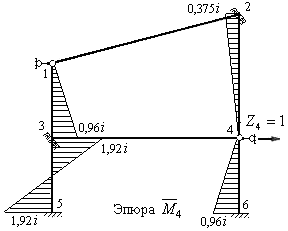
Рис.8.69
- Загружаем основную систему заданными нагрузками и строим грузовую эпюру изгибающих моментов 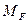 , используя формулы п. 6 § 8.6 для стержня 3-4 и формулы п. 8 § 8.6 (частный случай) для стержня 1-2 (рис.8.70).
, используя формулы п. 6 § 8.6 для стержня 3-4 и формулы п. 8 § 8.6 (частный случай) для стержня 1-2 (рис.8.70).
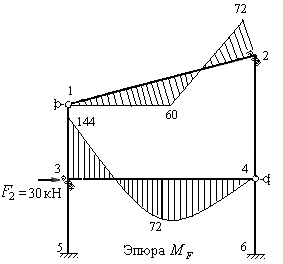
Рис.8.70
6) Определяем коэффициенты и грузовые реакции канонических уравнений статическим методом равновесия дисков или узлов, в зависимости от того, являются ли определяемые неизвестные сосредоточенными силами или сосредоточенными моментами.
Коэффициенты и грузовая реакция первого канонического уравнения являются сосредоточенными силами, возникающими в шарнирно стержневой связи 1 основной системы, загруженной последовательно единичным смещениям шарнирно стержневой связи 1, единичными углами поворота узлов 2 и 3, единичным смещениям шарнирно стержневой связи 4, а также заданными внешними нагрузками.
Для их определения вырезаем последовательно диск 1-2 из всех пяти эпюр изгибающих моментов, построенных в основной системе. Загружаем его, как показано на рис.8.71, составляем уравнения равновесия и вычисляем неизвестные коэффициенты и грузовые реакции первого канонического уравнения.
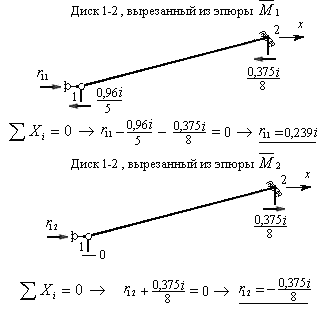
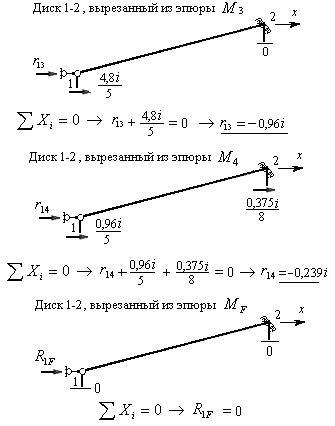
Рис.8.71
Коэффициенты и грузовая реакция второго и третьего канонических уравнений являются сосредоточенными реактивными моментами, возникающими в плавающих заделках 2 и 3 основной системы, загруженной последовательно единичным смещением шарнирно стержневой связи 1, единичными углами поворота узлов 2 и 3, единичным смещением шарнирно стержневой связи 4, а также заданными внешними нагрузками.
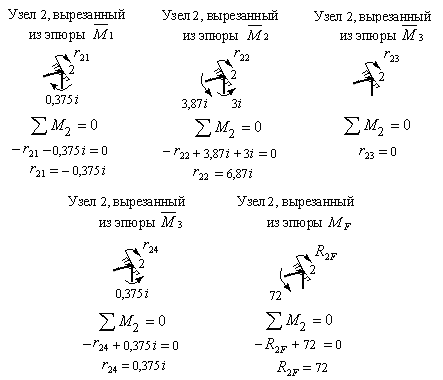
Рис.8.72
Для их определения вырезаем последовательно узел 2, а затем узел 3 из всех пяти эпюр изгибающих моментов, построенных в основной системе. Загружаем их, как показано на рис.8.72 и 8.73, составляем уравнения равновесия и вычисляем неизвестные коэффициенты и грузовые реакции второго и третьего канонических уравнений.
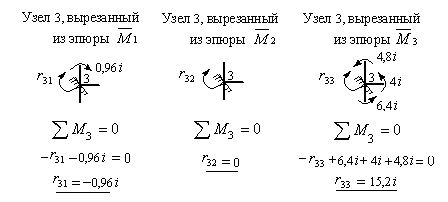
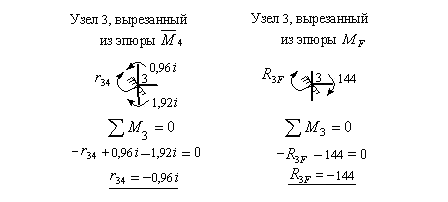
Рис.8.73
Коэффициенты и грузовая реакция четвертого канонического уравнения являются сосредоточенными силами, возникающими в шарнирно стержневой связи 4 основной системы, загруженной последовательно единичным смещениям шарнирно стержневой связи 1, единичными углами поворота узлов 2 и 3, единичным смещениям шарнирно стержневой связи 4, а также заданными внешними нагрузками.
Для их определения вырезаем последовательно диск 3-4 из всех пяти эпюр изгибающих моментов, построенных в основной системе. Загружаем его, как показано на рис.79, составляем уравнения равновесия и вычисляем неизвестные коэффициенты и грузовые реакции четвертого канонического уравнения.
7) Подставляем вычисленные значения коэффициентов и грузовых реакций в канонические уравнения и переносим грузовые реакции в их правые части. В результате получаем:
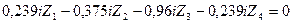
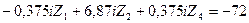
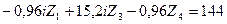
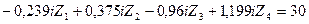
Из решения этой системы уравнений методом определителей, используя программу «Microsoft Excel» ПК находим:
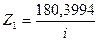 ,
, 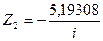 ,
, 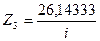
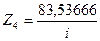
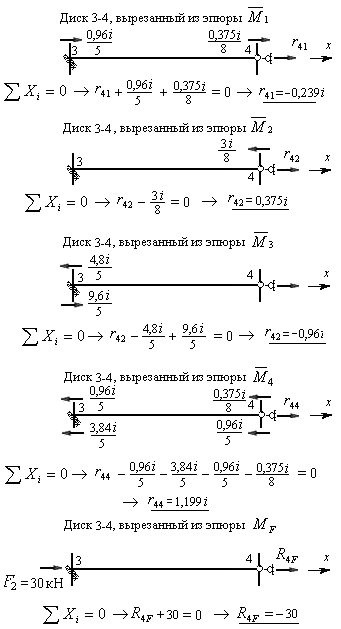
Рис.8.74
8) Строим исправленные эпюры 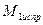 ,
, 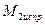 ,
, 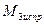 и
и 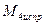 изгибающих моментов в основной системе путем умножения ординат единичных эпюр на вычисленные значения линейных смещений и углов поворота жестких узлов рамы (рис.8.75 – 8.78).
изгибающих моментов в основной системе путем умножения ординат единичных эпюр на вычисленные значения линейных смещений и углов поворота жестких узлов рамы (рис.8.75 – 8.78).
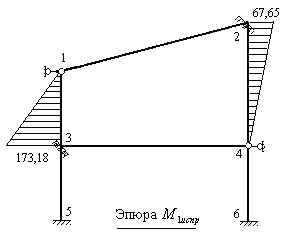
Рис.8.75
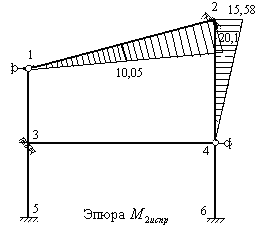
Рис.8.76
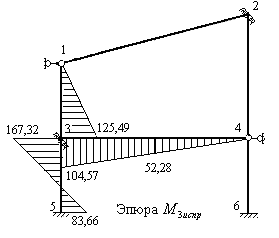
Рис.8.77
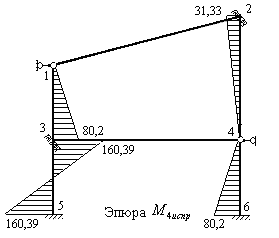
Рис.8.78
9) Вычисляем изгибающие моменты в характерных сечениях каждого стержня заданной рамы. Для этого находим алгебраические суммы ординат пяти эпюр: грузовой эпюры и четырех исправленных эпюр, построенных в основной системе метода перемещений. На рис 8.79 построена эпюра изгибающих моментов в заданной раме.
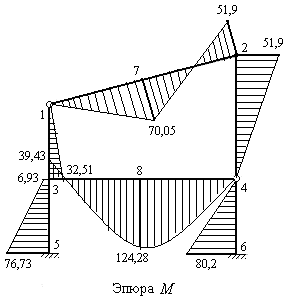
Рис.8.79
10) Статическая проверка эпюры изгибающих моментов выполняется. Суммы моментов, действующих на жесткие узлы 2 и 3 заданной рамы равны нулю, что следует из рис.8.79.
11) Вычисляем поперечные силы на каждом участке рамы, используя формулу Журавского и метод равновесия дисков.
Участок 3-5 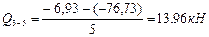
Участок 3-1 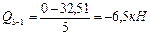
Участок 1-7 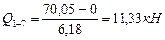
Участок 7-2 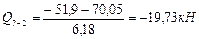
Участок 2-4 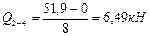
Участок 4-6 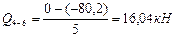
Участок 3-4 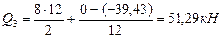
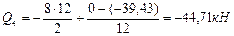
Строим эпюру поперечных сил 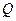 (рис.8.80).
(рис.8.80).
Рис.8.80
12) Вычисляем продольные силы на участках наклонного стержня и в других стержнях рамы, пользуясь методом равновесия узлов.
Вырезаем последовательно узлы 1, 2, 3, 4. Загружаем их силами, как показано на рис.8.81, составляем уравнения равновесия каждого узла и определяем неизвестные продольные усилия:
Узел 1 (tg 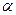 =0,25, cos
=0,25, cos 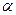 =0,9701, sin
=0,9701, sin 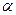 =0,2425)
=0,2425)
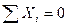

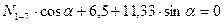

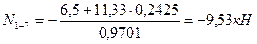


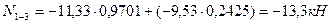
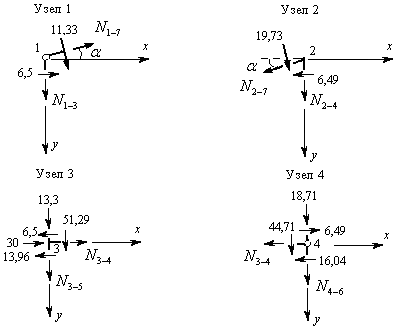
Рис.8.81
Узел 2 (tg 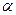 =0,25, cos
=0,25, cos 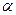 =0,9701, sin
=0,9701, sin 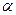 =0,2425)
=0,2425)