Алгебраическая сумма узловых изгибающих моментов в каждом жестком узле рамы должна быть равною нулю.

Если статическая проверка эпюры изгибающих моментов выполняется для каждого жесткого узла заданной рамы, то можно утверждать, что эпюра изгибающих моментов в заданной раме построена правильно.

Для выполнения деформационной проверки эпюры изгибающих моментов в заданной раме необходимо образовать основную систему метода сил (любой вариант) и построить одну из единичных эпюр в этой системе. Затем перемножить по правилу Верещагина эпюру изгибающих моментов в заданной раме на единичную эпюру в основной системе метода сил. Если результат перемножения равен нулю, то деформационная проверка выполняется.

8.12 Определение поперечных сил и построение эпюры

При определении поперечных сил необходимо рассматривать участки рамы свободные от распределенных нагрузок и участки, загруженные распределенными нагрузками. На участках рамы, свободных от распределенных нагрузок, эпюра изгибающих моментов в заданной раме всегда прямолинейна и поперечные силы имеют постоянные значения, определяемые по формуле Журавского:

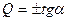, (8.10)

где 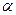- острый угол наклона эпюры изгибающих моментов к оси стержня. Знак плюс принимается в том случае, когда эпюру моментов необходимо повернуть против часовой стрелки на острый угол, чтобы она совместилась с осью стержня.

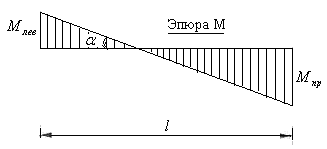
Рис.8.22

На рис.8.22 показана эпюра изгибающих моментов на одном из участков рамы. Поперечная сила на этом участке будет иметь постоянное значение на всем участке со знаком плюс.

Вычисляем поперечную силу по формуле (8.10).

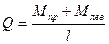(8.11)

На участках рамы, загруженных распределенной нагрузкой 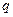эпюра изгибающих моментов криволинейна. Поперечные силы меняются по уравнению прямой, наклоненной к оси стержня под углом, тангенс которого равен интенсивности заданной распределенной нагрузки. При этом поперечная сила в начале участка определяется по формуле (8.12), а в конце участка - по формуле (8.13).

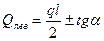(8.12)

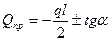(8.13)

При построении эпюры 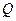ординаты со знаком плюс откладывают вверх от осей горизонтальных стержней и влево от осей вертикальных стержней. Ординаты эпюры 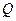со знаком минус откладывают вниз от осей горизонтальных стержней или вправо от осей вертикальных стержней.

8.13 Определение продольных сил и построение эпюры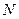

Продольные силы в стержнях заданной статически неопределимой рамы вычисляют статическим методом из условий равновесия узлов (аналогично, как и в методе сил).

Для этого сначала вырезают узлы рамы, которые объединяет только два стержня. Эти узлы загружают:

- неизвестными продольными усилиями в рассеченных стержнях (эти усилия направляют от узлов вдоль осей рассеченных стержней);

- заданными сосредоточенными узловыми силами (если они заданы в условии задачи);

- известными поперечными силами в тех же сечениях стержней. Величины и направления поперечных сил устанавливают по эпюре Q. Если поперечная сила имеет знак плюс, то её направляют так, чтобы она вращала узел по часовой стрелке. Если же поперечная сила имеет знак минус, то её направляют противоположно движению часовой стрелки.

Для каждого узла составляют два уравнения равновесия, используя рациональные условия равновесия, и определяют неизвестные продольные силы в рассеченных стержнях рамы.

Затем вырезают узлы, объединяющие три стержня, в одном из которых усилие уже определено и условий равновесия соседнего узла. В зависимости от знака этого усилия его направляют от узла, если усилие имеет знак плюс, или к узлу, если усилие имеет знак минус. Неизвестные продольные усилия направляют от узлов, догружают их поперечными силами в рассеченных стержнях и составляют для каждого узла два уравнения равновесия, из решения которых определяют неизвестные продольные усилия в рассеченных стержнях.

При построении эпюры продольных усилий принято откладывать перпендикулярно к осям стержней половины ординат в обе стороны от осей. Эпюра 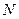является симметричной относительно оси каждого стержня рамы.