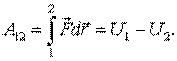В потенциальном поле работа сил поля на любом замкнутом пути равна нулю.
Работа. Мощность. Потенциальное поле сил. Кинетическая и потенциальная энергия
Источник – Детлаф, Яворский 2002г. Глава 3 п.п. 3.1 – 3.4. С. 33-47.
Элементарная работа силы 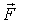 на перемещении
на перемещении 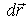
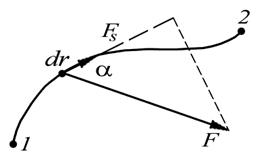 Рис. 7.1.Определение работы силы
Рис. 7.1.Определение работы силы
| 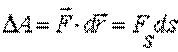 (7.1) (7.1)
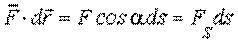

|
Величина 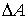 - алгебраическая. Единицей измерения работы в СИ служит Джоуль, сокращенное обозначение Дж.
- алгебраическая. Единицей измерения работы в СИ служит Джоуль, сокращенное обозначение Дж.
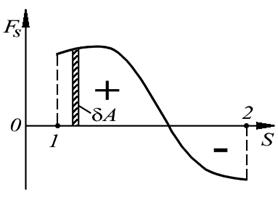
| 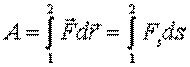 (7.2) (7.2)
|
| Рис. 7.2.Графический смысл работы сил |
ПРИМЕР 1
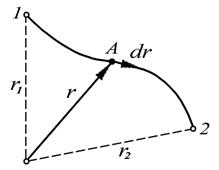
Найдем работу упругой силы 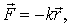 где
где 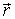 - радиус-вектор частицы А относительно точки О (рис. 7.7).
- радиус-вектор частицы А относительно точки О (рис. 7.7).
| 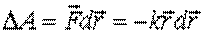
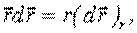


|
| Рис. 7.3.Работа упругой силы |
Тогда, работа данной силы на всем пути:
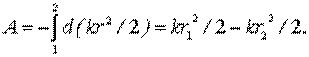
| (7.3) |
ПРИМЕР2.
Рассмотрим работу однородной силы тяжести 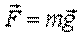 . Представим
. Представим 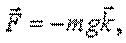 где орт вертикальной оси z с положительным направлением обозначен
где орт вертикальной оси z с положительным направлением обозначен 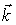 (рис.7.4).
(рис.7.4).
Элементарная работа силы тяжести на перемещении 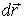
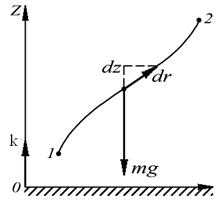
| 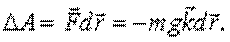 (7.4) (7.4)
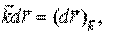
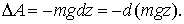
|
| Рис. 7.4. Работа однородной силы тяжести |
Работа же данной силы на всем пути от точки 1 до точки 2
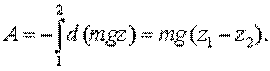
| (7.5) |
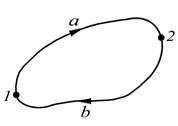
Стационарное силовое поле, в котором работа силы поля на пути между двумя любыми точками не зависит от формы пути, а зависит только от положения этих точек, называется потенциальным, а сами силы - консервативными.
В потенциальном поле работа сил поля на любом замкнутом пути равна нулю.
| 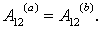 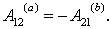
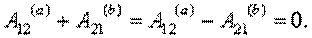
|
| Рис. 7.5. Работа в потенциальном поле сил |
Поле центральных сил. Потенциальная энергия
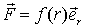 , ,
| (7.8) |
где 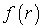 -функция, зависящая при данном характере взаимодействия только от r - расстояния между частицами;
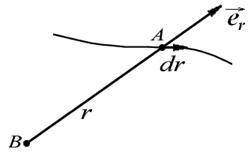
-функция, зависящая при данном характере взаимодействия только от r - расстояния между частицами; 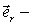 единичный вектор, задающий направление радиус-вектора частицы А относительно частицы В (рис.8.6).
единичный вектор, задающий направление радиус-вектора частицы А относительно частицы В (рис.8.6).
| 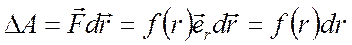
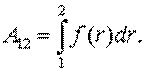
|
| Рис. 7.6. Работа в поле центральных сил |
Работа сил потенциального поля дает возможность ввести чрезвычайно важное понятие потенциальной энергии.
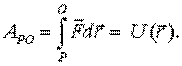
| (7.9) |
Функцию 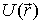 называют потенциальной энергией частицы в данном поле.
называют потенциальной энергией частицы в данном поле.
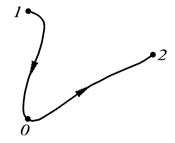
| Работа на пути 1O2 может быть представлена в виде 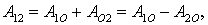 или, с учетом (7.9)
или, с учетом (7.9)
| ||
| Рис. 7.7. Введение понятия потенциальной энергии |
Работа сил поля на пути 1-2 равна убыли потенциальной энергии частицы в данном поле. Как только фиксирована потенциальная энергия в какой-либо точке, значения ее во всех остальных точках поля однозначно определяются формулой (7.10). Примеры рассмотрения потенциальной энергии различных силовых полей – Детлаф. Яворский, 2002 г., Глава 7. п.п. 7.7 С. 40 – 42 – самостоятельно.
Если на частицу в процессе движения действуют несколько сил, 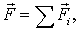 то
то
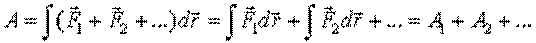
| (7.6) |
| <== предыдущая лекция | | | следующая лекция ==> |
| | | Для того чтобы произвольная ось вращения тела сохраняла свое направление неизменным, к ней необходимо приложить определенные силы. |
Дата добавления: 2017-06-02; просмотров: 4064;