Схема Бернулли. Формула Бернулли
1. Схема Бернулли. Формула Бернулли
Пусть производится n независимых однотипных испытаний, в каждом из которых событие А может появиться с вероятностью Р. Тогда вероятность непоявления события А, т.е. Р( 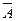 ) равна q=1-p.
) равна q=1-p.
Вероятность того, что событие А произойдет в этих n независимых испытаниях ровно k раз, можно вычислить по формуле Бернулли
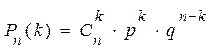
Для определения вероятности появления события A менее m раз (k < m), более m раз (k > m), хотя бы один раз ( 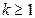 ) и т. п. могут быть использованы формулы:
) и т. п. могут быть использованы формулы:
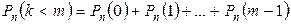 ,
,
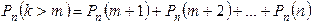 ,
,
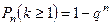 .
.
Пример: Прибор состоит из пяти узлов. Надежность (вероятность безотказной работы в течение времени t ) для каждого узла равна 0,9. Узлы выходят из строя независимо один от другого. Найти вероятность того, что за время t откажут ровно два узла.
Решение: Рассмотрим событие А - выход узла из строя за время t. Число узлов n=5. Число отказавших узлов за время t: k=2.
Р(А) - вероятность выхода узла из строя: p =P(A)=0,1. Тогда q=1-p=1-0,1=0,9.
Теперь вычислим искомую вероятность по формуле Бернулли:
Р5(2) = 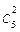 (0,1)2 .(0,9)3=10.0,01.0,729=0,0729.
(0,1)2 .(0,9)3=10.0,01.0,729=0,0729.
Пример .Всхожесть семян данного растения равна 90 %. Найти вероятность того, что из четырех посеянных семян взойдут: а) три; б) не менее трех.
Решение
а) Искомую вероятность находим с помощью формулы Бернулли (14), учитывая что 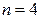 ,
, 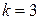 ,
, 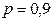 ,
, 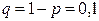 .
.
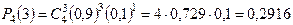 .
.
б) «Не менее трех» означает, что из четырех семян взойдут или три, или четыре. Так как эти события несовместны, то по теореме сложения искомая вероятность равна
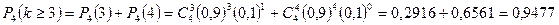 .
.
Дата добавления: 2017-06-02; просмотров: 3366;
