Вероятность безотказной работы резервированных восстанавливаемых систем
Для определения вероятности безотказной работы резервированной системы необходимо составить и решить систему дифференциальных уравнений ее функционирования.
Для системы с постоянно включенным резервом:
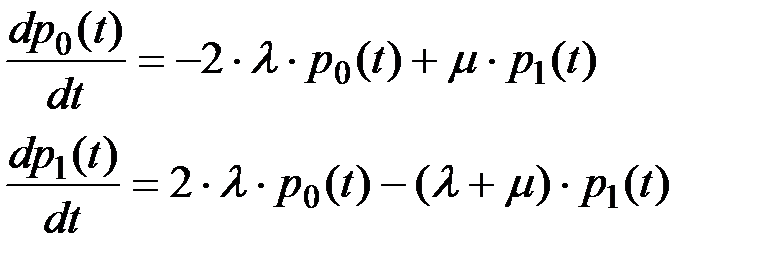(8.36)
Для системы с резервированием замещением:
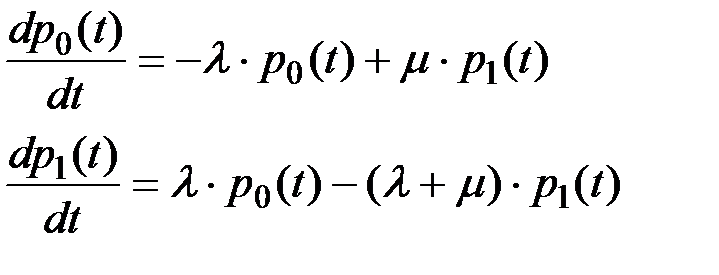(8.37)
При начальных условиях: р0(0)=1, р1(0)=0.
Неремонтируемаярезервированная система.
Вероятность безотказной работы системы при постоянно включенном резерве:
(8.38)
Средняя наработка до отказа:
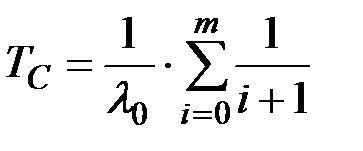(8.39)
Вероятность безотказной работы резервированной системы замещением:
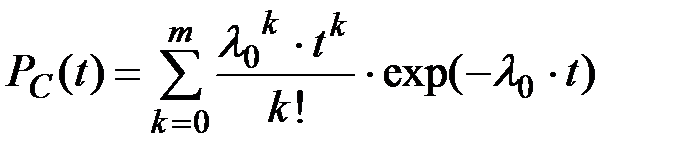(8.40)
Средняя наработка на отказ:
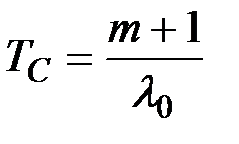(8.41)
где m –– число резервных элементов; l0 –– интенсивность отказов каждого из элементов системы, включая основной.
Пример результатов расчетов среднего времени наработки на отказ резервированных неремонтируемых систем при различном числе резервных элементов представлен в табл. 8.7.
Таблица 8.7
Среднее значение времени наработки на отказ резервированных невосстанавливаемых систем при интенсивности отказов одного устройства (как основного, так и резервных) l0=0.03 1/час.
| Наработка на отказ | m=0 | m=1 | m=2 | m=3 | m=4 |
| ТС (горячее), час | 33.3 | 61.1 | 69.4 | 76.1 | |
| ТС (холодное), час | 33.3 | 66.7 | 133.3 | 166.7 |
Ремонтируемая резервированная система.
Определение вероятности безотказной работы ремонтируемой резервированной системы является весьма сложной задачей.
Далее рассматриваются толькодублированныесистемы.
Вероятность безотказной работы ремонтируемой системы при постоянно включенном резервеопределяется соотношением:
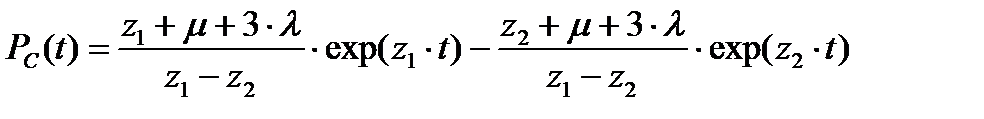(8.42)
где
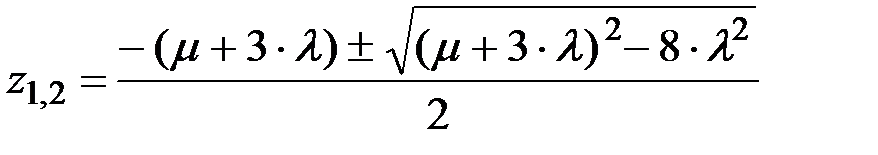(8.43)
Средняя наработка до отказа:
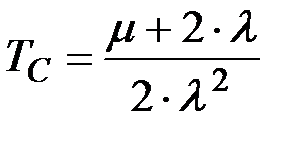(8.44)
Вероятность безотказной работы дублированной ремонтируемой системы, резервированной замещением:
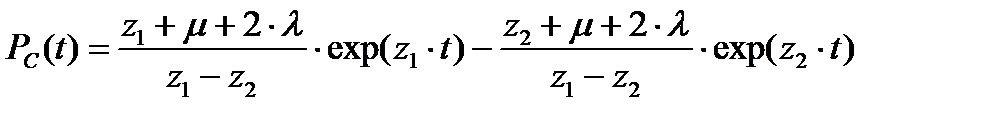(8.45)
где
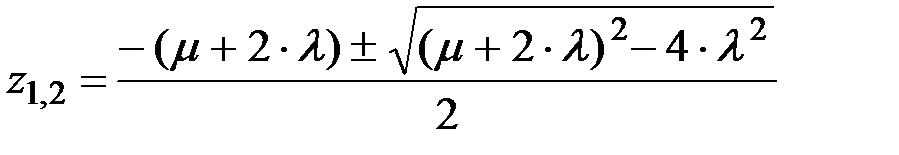(8.46)
Средняя наработка на отказ:
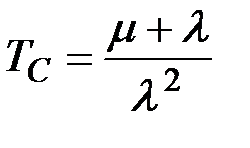(8.47)
В формулах (8.42)…(8.47): l –– интенсивность отказов, а m –– интенсивность восстановлений каждого устройства рассматриваемой дублированной системы.
Пример 8.3. Расчет надежности дублированных восстанавливаемых технических систем.
Даны технические системы дублированные по способу постоянно включенного резерва (горячее резервирование) и по способу замещения (холодное резервирование). Интенсивность отказов устройств l = 0.03 (1/час), интенсивность восстановления m = 0.1 (1/час).
Требуется определить изменение надежности систем в течение 100 часов работы. Определить среднее время работы систем до отказа.
Расчеты выполняются по формулам (8.42)…(8.47).
Время наработки на отказ при «горячем» резервировании ТС=88.9 час.
Время наработки на отказ при «холодном» резервировании ТС=144.4 час.
Изменение вероятности безотказной работы систем во времени представлены в табл. 8.8.
Таблица 8.8.
Надежность дублированных восстанавливаемых систем.
| Время работы системы, час | Надежность при «горячем» резервировании | Надежность при «холодном» резервировании |
| 0.8653 | 0.9230 | |
| 0.7097 | 0.8228 | |
| 0.5810 | 0.7322 | |
| 0.4758 | 0.6516 | |
| 0.3895 | 0.5797 |
Выигрыш в среднем времени наработки на отказ дублированной системы за счет восстановления для постоянно включенного резерва и резерва замещением равен соответственно:
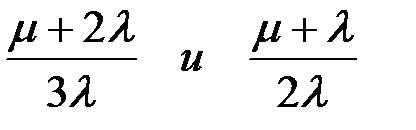(8.48)
Зависимости (8.48) получены делением ожидаемого времени наработки на отказ восстанавливаемой (8.44), (8.47) системы на ожидаемое время наработки на отказ (8.39), (8.41) соответствующей системы без восстановления.
| Вероятность безотказной работы Д У Б Л И Р О В А Н Н Ы Х ремонтируемых систем при интенсивности отказов 0.39 (1/год) |
| Резервирование с постоянно включенным резервом |
| Резервирование замещением |
Результат решения, выполненный в среде Mathcad
Кривые изменения надежности рассматриваемых технических систем свидетельствуют о преимуществах (по показателям надежности) резервирования замещением перед резервированием с постоянно включенным резервом.
Пример 8.4.
Рассмотрим систему, у которой один из элементов может восстанавливаться (ремонтироваться) [13].
Размеченный граф такой системы представлен на рис. 8.9.
Система состоит из двух элементов. Состояние S0 (вероятность нахождения системы в момент t в этом состоянии P0(t)) соответствует сохранению работоспособности обоих элементов. Состояние S1 (P1(t)) – отказ одного первого элемента, но сохранение работоспособности системы за счет работы второго элемента. Состояние S2 (P2(t)) - отказ второго элемента и поступление его в ремонт. Если в нерабочем состоянии находятся оба элемента, то наступает состояние S3 (P3(t)) – система выходит из строя.
Система дифференциальных уравнений Колмогорова:
+ 
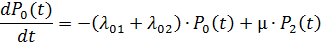
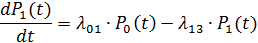
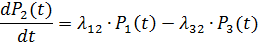
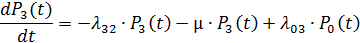
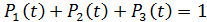
| Расчет в системе Mathcad надежности технической системы с одним ремонтируемым элементом. При этом введены новые обозначения интенсивностей отказов. |
Z:=rkfixed(x,0,5000,99,D)
Интенсивности отказов элементов: λ0,2=10-3, λ0,1=10-3, λ1,3=2∙10-2, λ2,3=5∙10-3, интенсивность восстановления второго элемента µ=2∙10-5 . Учитывая, что расчетный интервал времени выбран в пределах (0…5000 час) и число интервалов дробления равно 100, получим возможность определить вероятность отказа системы через время t(час) [15]:
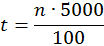
В частности, вероятность отказа рассматриваемой системы Q(t)=0.9 наступит через t=2700 часов.
Ниже представлен результат решения примера 8.4. по нахождению вероятности P3(t) попадания системы в нерабочее состояние (в состояние S3).
Пример 8.5.
Для снабжения энергией поселка требуется мощность 1000 кВт, что обеспечивается работой четырех агрегатов (n=4) по 100 кВт каждый с коэффициентом простоя qn=0.04 и трех (m=3) агрегатов по 200 кВт каждый с коэффициентом простоя qm-0.05.
Коэффициент простоя отождествляется с коэффициентом неготовности системы, т.е. например,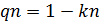 
, где kn – коэффициент готовности.
Требуется определить ожидаемый недоотпуск энергии.
Решение примера 8.5 в среде Matlab.
n=4;m=3;Mn=100;Mm=200;
qn=0.04;qm=0.05;
Qn=1-(1-qn)^n; Вероятность отказа хоть одного агрегата из группы «n»
Qm=1-(1-qm)^m; Вероятность отказа хоть одного агрегата из группы «m»
M1=Qn*Mn; Вероятный недоотпуск энергии группой «n»
M2=Qm*Mm; Вероятный недоотпуск энергии группой «m»
Q=Qn*Qm; Вероятность одновременного простоя хотя бы по одному агрегату из обеих групп
MM=Q*(Mn+Mm); Ожидаемый недоотпуск энергии в случае одновременного простоя хотя бы по одному агрегату из обеих групп
[Qn,Qm,Q,M1,M2,MM] Результат решения
ans = 0.1507 0.1426 0.0215 15.0653 28.5250 6.4461
Анализ результатов решения примера 8.5. может вызвать удивление. Недоотпуск энергии при простое агрегатов из обеих групп меньше, чем при простое агрегатов из одной группы. Ответ очень прост: вероятность простоя хотя бы одного агрегата из одной группы больше, чем вероятность простоя хотя бы одного агрегата из обеих групп одновременно, а в итоге рассчитывается ожидаемый (вероятный) недоотпуск энергии.
Подобные задачи распространены на этапах проектирования для определения предполагаемых штрафных санкций.
Вопросы для самоконтроля.
Объясните значение коэффициента готовности технической системы.
Объясните значение функции готовности технической системы.
Дайте пример использования коэффициента готовности технической системы.
Какой вид резервирования восстанавливаемых технических систем наиболее эффективен по показателям надежности.
Дата добавления: 2019-02-07; просмотров: 2122;