Аналитическое решение системы дифференциальных уравнений.

Ниже приводится один из методов решения системы дифференциальных уравнений.

Рассмотрим систему, состоящую из одного ремонтируемого элемента и имеющую два состояния:

S₀(t) –– система в момент t находится в рабочем состоянии;

S₁(t) –– система в момент t находится в ремонте ( не работает).

Система уравнений Колмогорова имеет вид:

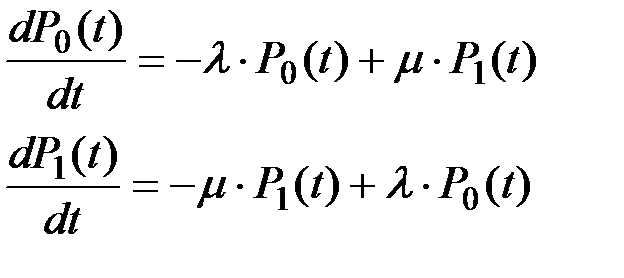(П1.35)
Найдем интеграл этой системы уравнений, для чего введем обозначения P₀(t)=y, P₁(t)=z.

Тогда система уравнений принимает вид:

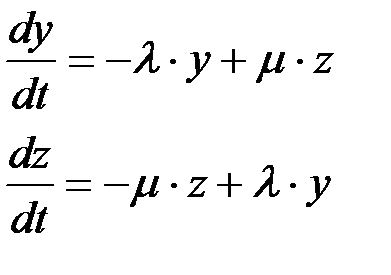(П1.36)
Дифференцируем первое уравнение:

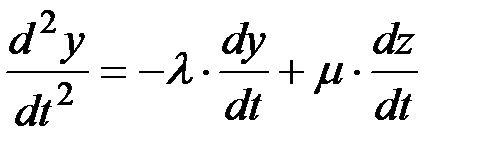(П1.37)
Из первого же уравнения находим z:

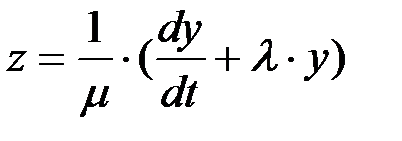(П1.38)
Из второго уравнения системы после подстановки найденного выражения для z имеем:

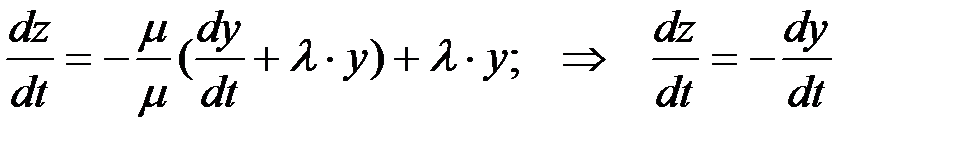(П1.39)
Подставляем полученное выражение производной (П1.39) в уравнение (П1.37), получим:

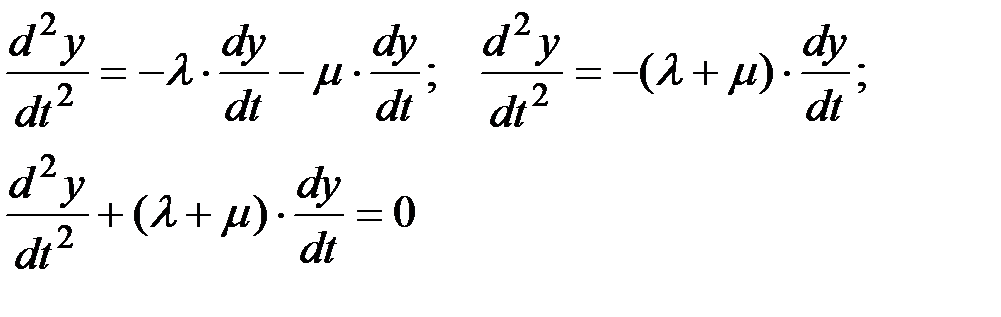(П1.40)
Характеристическое уравнение имеет вид:

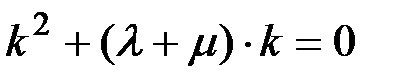(П1.41)
Решение характеристического уравнения дает корни:

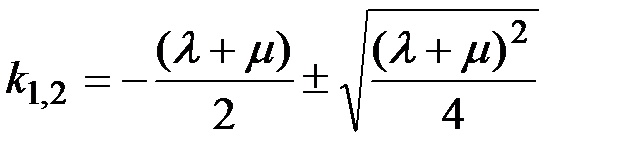, откуда

k₁=0, k₂=-(l+m) (П1.42)
Общее решение системы однородных дифференциальных уравнений при вещественных и неравных корнях имеет вид:

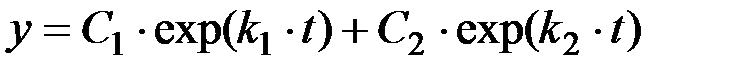, (П1.43)
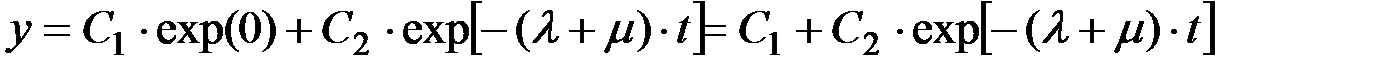(П2.10)

Учитывая начальные условия

y(0)=1 z(0)=0 (П1.44)
получим:

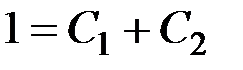(П1.45)
Тогда

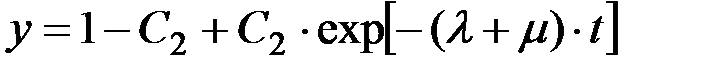(П1.46)
Дифференцируем (П2.10):

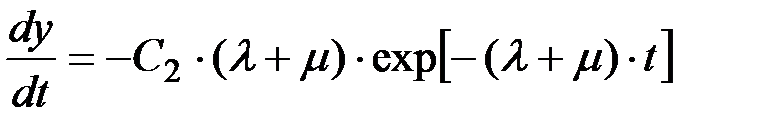(П1.47)
Подставляя в (П2.4) выражения (П2.13) и (П2.14), получим:

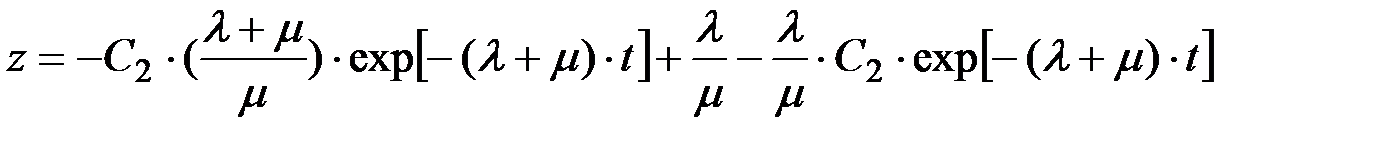(П1.48)

При подстановке начального условия z(0) = 0, получим уравнение:

,

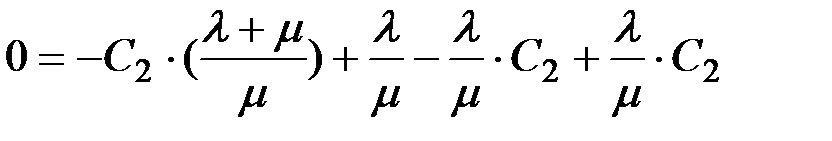откуда

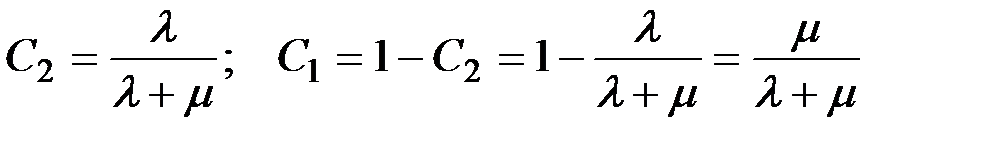(П1.49)
Подставляя (П2.16) в (П2.10) и (П2.15), получим окончательно:

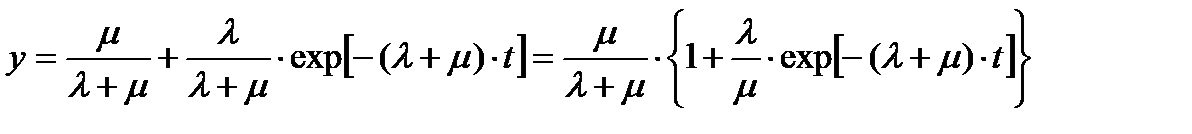(П1.50)
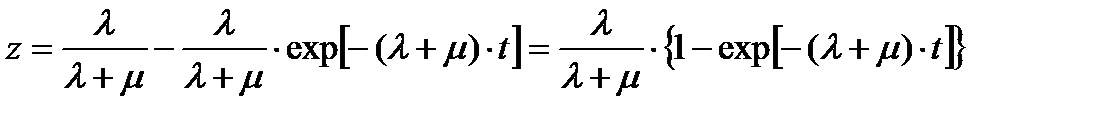(П1.51)

Кроме рассмотренного метода, могут использоваться и другие, например, с помощью преобразований Лапласа.

Заметим, что с пакетами Mathcad или Matlab системы дифференциальных уравнений интегрируются проще [16, 17, 18}.

Приложение 2.