П2.3. Формула полной вероятности
Если до проведения опыта вероятности реализации гипотез Н1, Н2,…, Нn были Р(Н1), Р(Н2),…, Р(Нn), и в результате опыта появилось событие А, то с учетом этого факта «новые», т.е. условные вероятности гипотез вычисляются по формуле Бейеса, которая дает возможность «пересмотреть» априорные вероятности гипотез с учетом результата проведенного опыта:
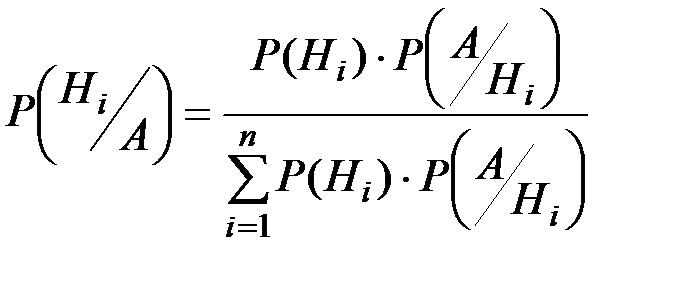 (П2.11)
(П2.11)
Если об обстановке опыта можно сделать n исключающих друг друга предположений (гипотез) Н1, Н2, …, Нn и если событие А может появиться только при одной из этих гипотез, то вероятность реализации события А вычисляется по формуле полной вероятности:
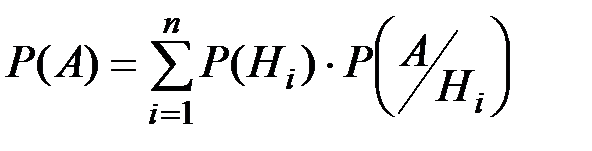 (П2.12)
(П2.12)
Если после опыта, закончившегося появлением события А, производится еще один опыт, в котором может появиться или не появиться событие В, то вероятность (условная) появления этого события вычисляется по формуле полной вероятности, в которую подставлены не прежние вероятности гипотез {Р(Hi)}, а новые { 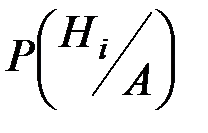 }:
}:
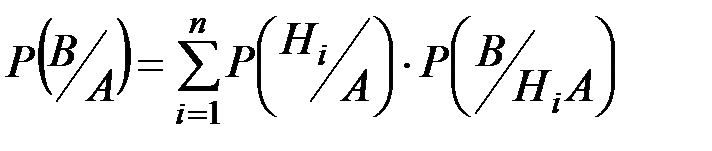 (П2.13)
(П2.13)
Задача П2.15.
Прибор контроля концентрации водорода в воздухе аккумуляторного цеха может работать в двух режимах: нормальном и аварийном. Нормальный режим наблюдается в 70% всех случаев работы прибора за время t, аварийный режим – в 30%. Вероятность выхода прибора из строя за время t в нормальном режиме равна 0.001, в аварийном режиме – 0.08. Найти в среде Matlab безусловную вероятность Р выхода прибора из строя за время t.
HN=0.7;HA=0.3;QN=0.001;QA=0.08;
Q=HN*QN+HA*QA
Q= 0.0247
Задача П2.16.
По железнодорожному мосту следуют грузовые и пассажирские поезда. При следовании пассажирского поезда вероятность поломки моста равна 0.001, при следовании грузового поезда –– 0.007. Пассажирские поезда следуют в 80%, грузовые –– 20%.
Найти безусловную вероятность поломки моста.
Ответ.
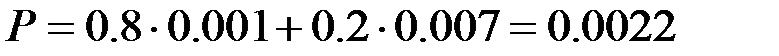
Задача П2.17.
Завод изготавливает изделия, каждое из которых с вероятностью р имеет дефект. В цехе имеются три контролера и каждое изделие осматривается одним из контролеров, который с вероятностью рi (i=1, 2, 3) обнаруживает дефект, если он имеется. С цеха изделия поставляются в отдел технического контроля (ОТК) завода, где проверяются все изделия и дефект (если он имеется) обнаруживается с вероятностью р0.
Определить:
вероятность того, что изделие будет забраковано (событие А);
вероятность того, что изделие будет забраковано контролером в цехе (событие В);
вероятность того, что изделие будет забраковано в ОТК завода (событие С).
Решение [8].
События В и С несовместны и событие А может наступить только в случае реализации события В или события С (изделие может быть забраковано либо контролером, либо в ОТК), т.е. А = В + С, следовательно:
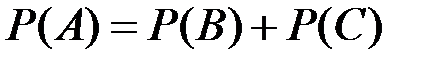
Находим вероятность того, что изделие будет забраковано одним из контролеров в цехе. Для этого необходимо, чтобы во-первых изделие было неисправным, и, во-вторых, чтобы этот дефект был обнаружен контролером.
Вероятность того, что данное изделие попадет к данному контролеру равна 1/3, т.е. вероятности 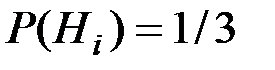 . Вероятность того, что изделие будет забраковано одним из контролеров (при условии, что данное изделие неисправно):
. Вероятность того, что изделие будет забраковано одним из контролеров (при условии, что данное изделие неисправно):
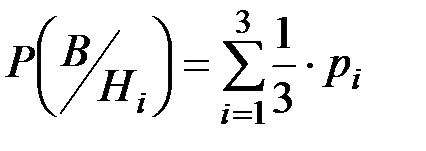
Безусловная вероятность того, что изделие неисправно и будет забраковано контролерами в цехе:
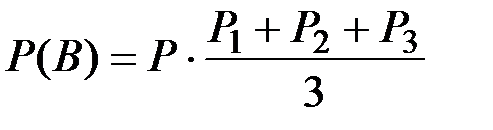
где Р –– вероятность того, что изделие неисправно.
Аналогично:
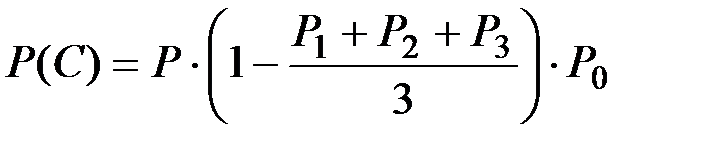
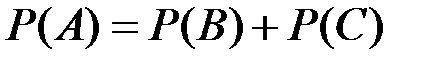
Пусть даны числовые значения:
Р=0.001, Р1 = 0.8, Р2 = 0.7, Р3 = 0.9, Р0 = 0.8.
Тогда
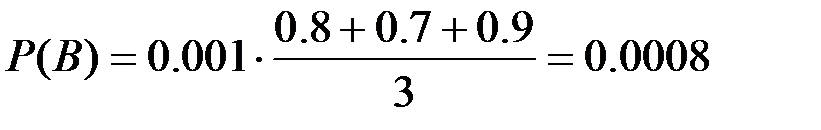
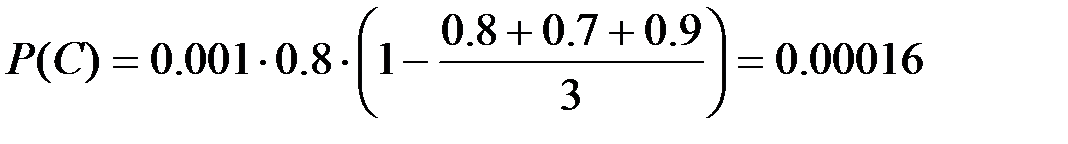
Задача П2.18.
Приборы одного наименования (однотипные приборы) изготавливаются двумя предприятиями. Первое предприятие производит 2/3 всех приборов, поступающих на рынок, второе –– 1/3. Надежность (вероятность безотказной работы) приборов первого предприятия равна Р1, второго –– Р2.
Определить надежность приборов, приобретаемых на рынке.
Ответ.
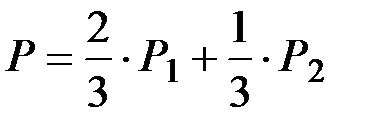
Задача П2.19.
Имеется две партии однотипных изделий. Первая партия состоит из N изделий, среди которых n дефектных. Вторая партия состоит из М изделий, среди которых m дефектных. Из первой партии берется случайным образом К изделий, из второй партии берется L (K<N, L<M). Эти K+L изделий смешиваются и образуется новая партия, из которой наугад берется одно изделие.
Найти вероятность того, что это изделие будет дефектным.
Решение.
Пусть событие А состоит в том, что выбрано дефектное изделие.
Гипотеза H1 –– изделие принадлежало первой партии,
Гипотеза H2 –– изделие принадлежало второй партии.
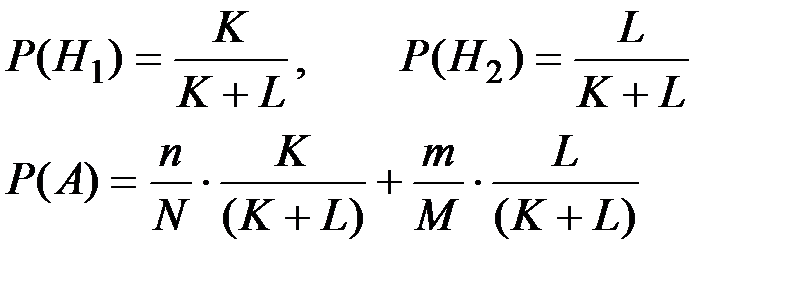
Задача П2.20.
Прибор состоит из двух дублирующих друг друга узлов. Прибор работает в воде и в воздухе. Надежность прибора при работе в воздухе равна р1, при работе в воде –– р2.
Вероятность того, что прибор будет работать в воздухе равна W, вероятность того, что прибор будет работать в воде равна (1-W).
Примечание. W может быть заменена отношением числа включений прибора в воздухе к общему числу включений прибора.
Требуется определить надежность прибора.
Ответ.
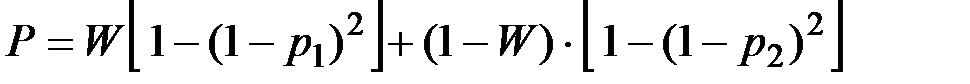
Задача П2.21.
Прибор состоит из двух узлов. Работа каждого узла безусловно необходима для работы прибора. Надежность (вероятность безотказной работы прибора в течение времени t) первого узла равна р1, второго –– р2. Прибор испытывается в течение времени t, в результате испытания прибор отказал.
Требуется определить вероятность того, что отказал первый узел, а второй остался исправным.
Решение [8].
До опыта возможны четыре гипотезы:
Н0 –– исправны оба узла;
Н1 –– отказал первый узел, второй –– исправен;
Н2 –– отказал второй узел, первый –– исправен;
Н3 –– отказали оба узла.
Вероятности реализации гипотез:

Вероятность того, что наблюдалось событие А –– прибор отказал:
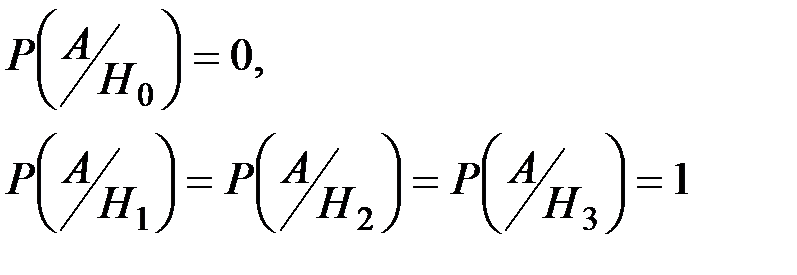
Формула Бейеса:
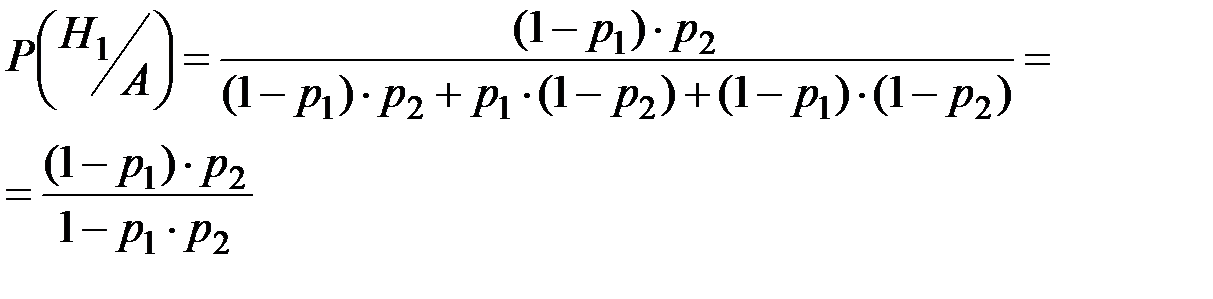
Задача П2.22.
Завод изготавливает изделия, каждое из которых с вероятностью р имеет дефект. В цехе изделие с равной вероятностью осматривается одним из двух контролеров. Первый контролер обнаруживает имеющийся дефект с вероятностью р1, второй –– с вероятностью р2. Если в цехе изделие не забраковано, оно поступает в отдел технического контроля завода (ОТК), где изделие, если оно имеет дефект, бракуется с вероятностью р0.
Директору предприятия приносят бракованное изделие. Директор дает команду рассчитать вероятность того, что изделие забраковано:
1) первым контролером,
2) вторым контролером,
3) ОТК завода.
Решение [8].
До опыта возможны четыре гипотезы:
Н0 –– дефектное изделие не забраковано;
Н1 –– изделие забраковано первым контролером;
Н2 –– изделие забраковано вторым контролером;
Н3 –– изделие забраковано ОТК завода.
Вероятность реализации события А состоит в том, что изделие забраковано 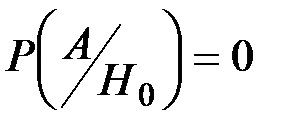
Поскольку изделие в цехе осматривается первым или вторым контролером с вероятностью ½, то априорные вероятности реализации гипотез:
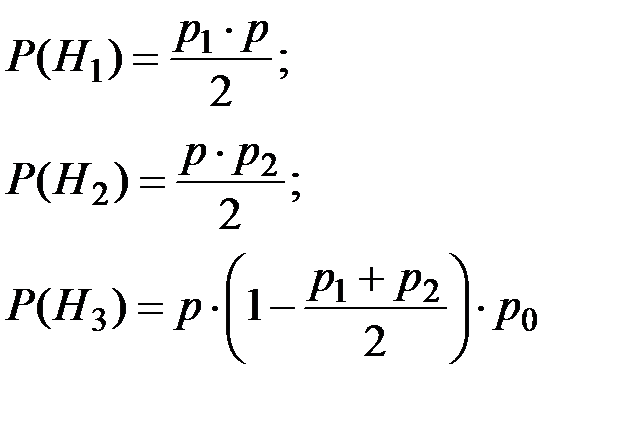
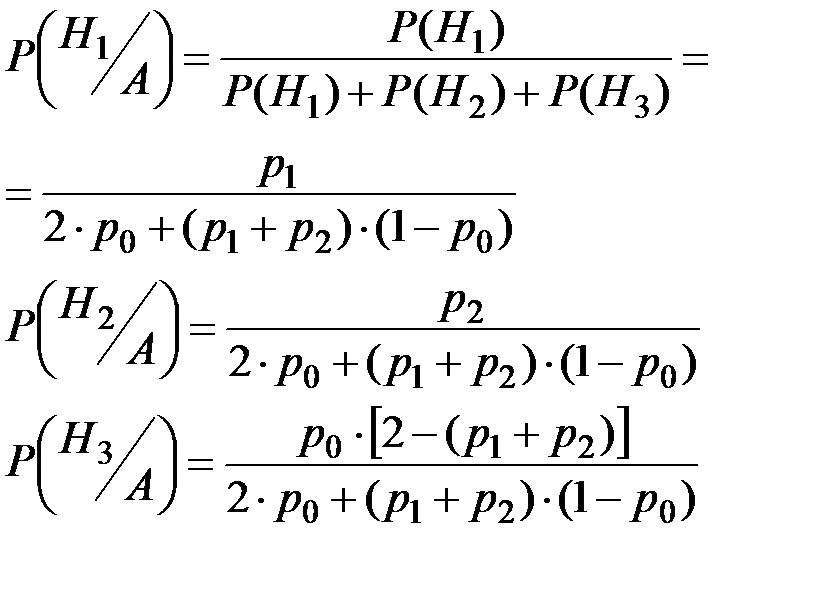
Дата добавления: 2019-02-07; просмотров: 1396;
