Теорема сложения вероятностей.
Суммой нескольких событий называется событие, состоящее в появлении хотя бы одного из них.
Произведением нескольких событий называется событие, состоящее в совместном появлении всех этих событий.
Для несовместных событий:
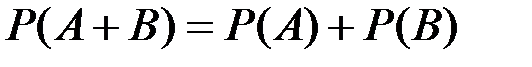 (П2.4)
(П2.4)
Для совместных событий:
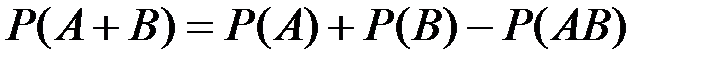 (П2.5)
(П2.5)
где Р(АВ) –– вероятность появления событий А и В одновременно.
Полной группой нескольких событий называется счетное множество событий, одно из которых непременно произойдет и не существует событий, выходящих за пределы рассматриваемого множества.
Если события Al…..An несовместны и образуют полную группу событий, то:
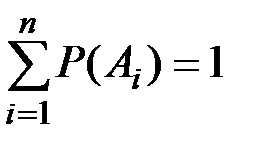 (П2.6)
(П2.6)
Сумма вероятностей противоположных событий равна 1:
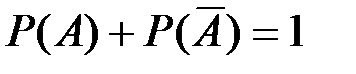 (П2.7)
(П2.7)
где 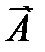 –– событие, противоположное событию А.
–– событие, противоположное событию А.
Условной вероятностью события A при наличии события B называется вероятность события A, вычисленная при условии, что событие B произошло. Эта вероятность обозначается 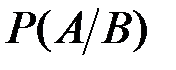 .
.
События A и B называются независимыми, если появление одного из них не меняет вероятность появления другого.
Для независимых событий
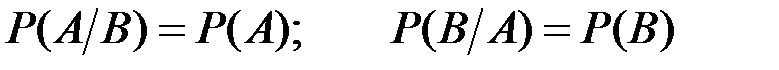 (П2.8)
(П2.8)
Теорема умножения вероятностей.
Вероятность произведения двух событий равна вероятности одного из них, умноженной на условную вероятность другого при наличии первого.
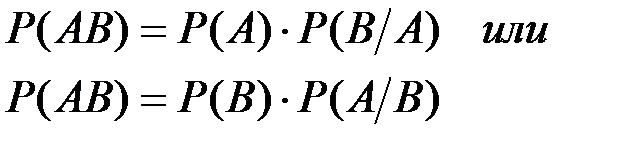 (П2.9)
(П2.9)
Для независимых событий:
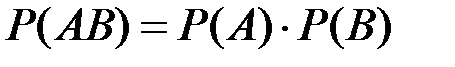 (П2.10)
(П2.10)
Задача П2.5.
Партия изделий состоит из a исправных и b неисправных. Выбирается одно изделие, проверяется на исправность и возвращается в эксперимент. После этого из партии берется еще одно изделие.
Найти вероятность того, что оба изделия будут исправными.
Ответ.
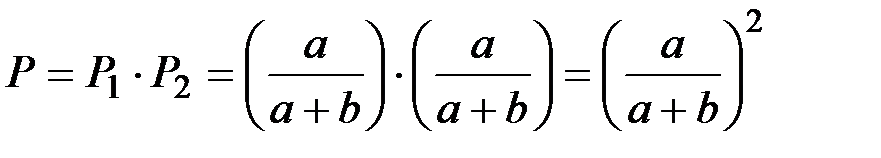
Задача П2.6.
Над изготовлением одного изделия последовательно работают 3 рабочих. Качество изделия при передаче следующему рабочему не проверяется. Первый рабочий допускает брак с вероятностью 0.05, второй – 0.08, третий – 0.03.
Найти в среде Mathcad вероятность того, что при изготовлении изделия будет допущен брак.
Задача П2.7.
Прибор состоит из n=3 последовательно соединенных блоков. Выход из строя любого блока означает выход из строя прибора. Блоки выходят из строя независимо друг от друга.
Интенсивность отказов каждого блока равна l=10-2 1/сутки.
Найти в среде Mathcad надежность прибора за t=110 суток работы.
Какова должна быть надежность каждого блока для обеспечения заданного уровня надежности прибора pp= 0.99.
Решение.
Задача П2.8.
Для повышения надежности прибора он резервируется еще тремя точно такими же приборами, включенными «параллельно». Интенсивность отказов каждого прибора 10-3 1/час. Определить в среде Matlab надежность системы за 150 часов работы.
L1=10^-3;t=150;m=3;
P1=exp(-L1*t);
Pt=1-(1-P1)^(m+1)
Pt=0.9996
Задача П2.9.
Для повышения надежности системы применена схема дублирования. Дублирующее устройство включается в работу в случае отказа основного с помощью коммутатора. Надежность основного устройства Р0 =0.85, дублирующего устройства равна pд =0.7, надежность коммутатора pк =0.55. Определить в среде Mathcad вероятность безотказной работы системы.
Задача П2.10.
Для повышения надежности прибора он резервируется m другими точно такими же приборами по способу постоянно включенного резерва. Надежность каждого прибора равна p=0.7. Определить в среде Mathcad, сколько надо включить приборов (каково число m), чтобы обеспечить заданную надежность Pтр =0.995 системы в целом.
| m=3 |
Задача П2.11.
В условиях задачи П2.10 для каждого дублирующего элемента применяется устройство переключения с одинаковой надежностью p1.
А. Определить надежность системы.
Б. Найти требуемое число дублирующих элементов при заданной (требуемой) общей надежности системы Ptr .
Ответ:
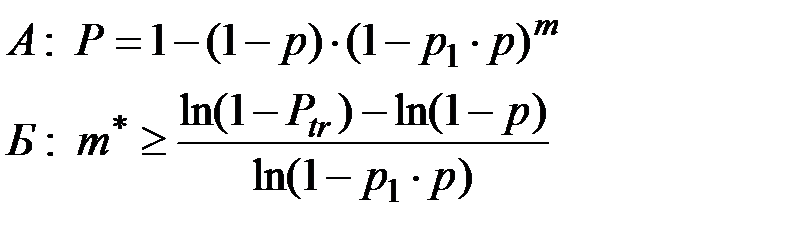
Задача П2.12.
Техническая система состоит из n блоков, надежность каждого из которых равна р. Выход из строя хотя бы одного блока влечет за собой выход из строя всей системы.
С целью повышения надежности системы производится дублирование, для чего выделено еще n таких же блоков. Надежность переключающих устройств равна единице.
Определить, какой способ дублирования дает более высокую надежность системы:
а) дублирование каждого блока
б) дублирование всей системы
Решение [8].
Надежность РА системы, дублированной по способу а), определяется по формуле:
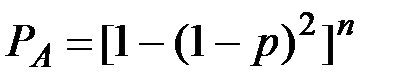 .
.
Надежность РБ системы, дублированной по способу б), имеет вид:
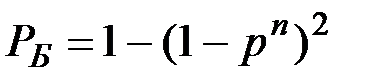
Покажем, что при любом n и 0 < p < 1 выполняется неравенство РА > РБ
Поскольку:
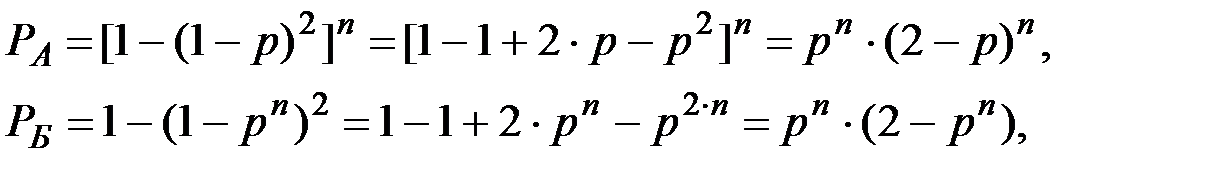
то достаточно доказать неравенство:
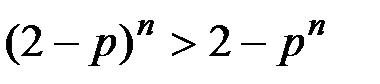
Положим 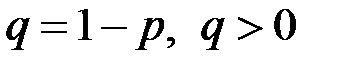 , тогда исследуемое неравенство примет вид:
, тогда исследуемое неравенство примет вид:
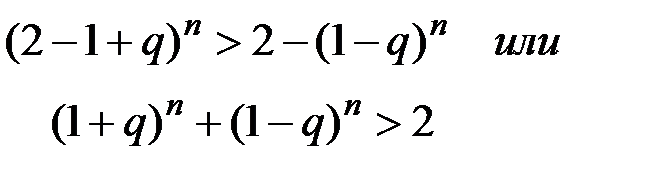
Применяя формулу бинома, и замечая, что все отрицательные члены разложения взаимно уничтожаются, получим:
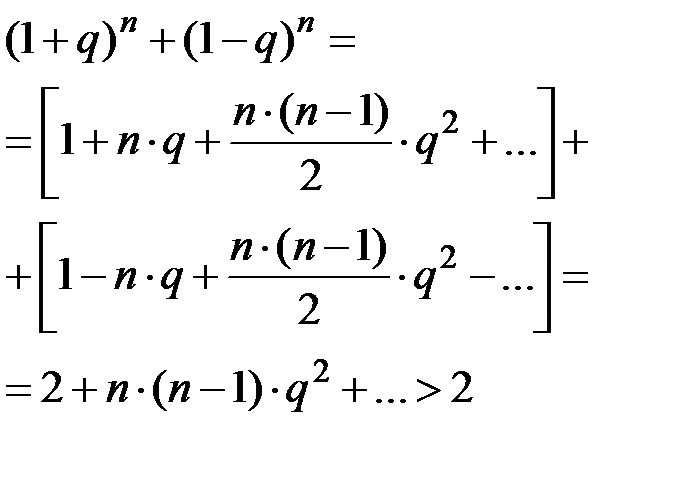
Что и доказывает справедливость неравенства, а вместе с ним и заключение о более высокой надежности системы при дублировании каждого элемента в сравнении с дублированием всей системы.
Задача П2.13.
В технической системе дублируются не все элементы, а только наименее надежные. Надежности отдельных узлов представлены на схеме.
Определить надежность всей системы.
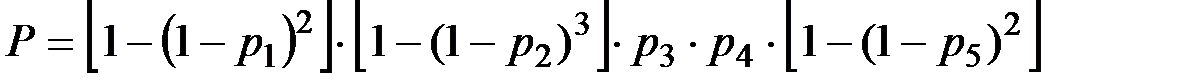
Задача П2.14.
Прибор состоит из трех блоков. В первом блоке n1 элементов, во втором n2 и в третьем n3 . Для работы прибора безусловно необходим первый узел, два других узла дублируют друг друга. Надежность всех составляющих элементов одинакова и равна р. Выход из строя одного элемента адекватен выходу из строя соответствующего блока. Элементы выходят из строя независимо друг от друга.
Определить надежность прибора.
Решение.
Надежность первого блока 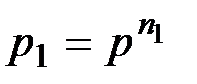
Надежность второго блока 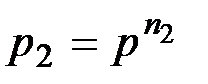
Надежность третьего блока 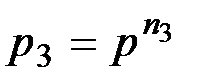
Надежность дублированной системы, состоящей из второго и третьего блоков:
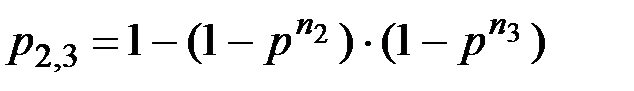
Надежность прибора:
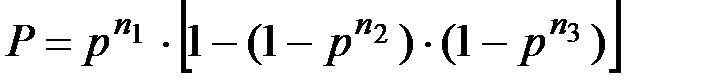
Дата добавления: 2019-02-07; просмотров: 875;
