Критерий совместности системы (теорема Кронекера-Капелли)

Пусть дана произвольная система, состоящая из m линейных уравнений с n неизвестными

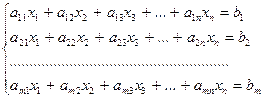
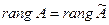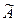Теорема 3.1. Для того, чтобы система линейных уравнений была совместна, необходимо и достаточно чтобы ранги основной и расширенной матриц были одинаковы, т.е. , где – расширенная матрица системы.

Доказательство необходимости.

Пусть существует решение системы (3.1) } – 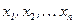,тогда эту систему можно представить в виде следующего равенства: , .

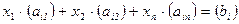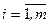Так как столбец свободных членов есть линейная комбинация столбцов, образующих основную матрицу, то число линейно независимых столбцов основной и расширенной матриц будет одинаковым. Следовательно, .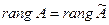

Доказательство достаточности.

Пусть ранг основной матрицы равен рангу расширенной матрицы и равен r. Предположим, что базисный минор расположен в левом верхнем углу расширенной матрицы, но тогда по теореме 2.1 (о базисном миноре) имеет место равенство 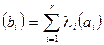, которое можно переписать в виде 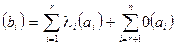. Однако последнее означает, что система (3.1) имеет решение 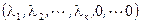, то есть она совместна.

Теорема доказана.

Следствия:

1) если 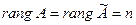( 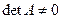), где n – число неизвестных, то система имеет единственное решение;

2) если 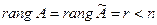, то система имеет бесчисленное множество решений, при этом 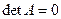, r неизвестных являются основными(базисными), а остальные n-r – свободными;

3) 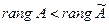, то система несовместна.