Теорема сложения математических ожиданий.
Математическое ожидание суммы случайных величин определяется по формуле:
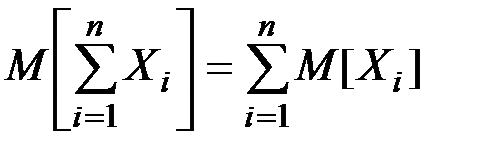 (П2.62)
(П2.62)
Математическое ожидание линейной функции нескольких случайных величин:
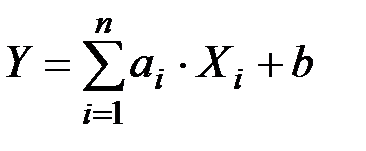 , где ai и b –– не случайные коэффициенты, равно той же линейной функции от их (случайных величин линейной функции) математических ожиданий:
, где ai и b –– не случайные коэффициенты, равно той же линейной функции от их (случайных величин линейной функции) математических ожиданий:
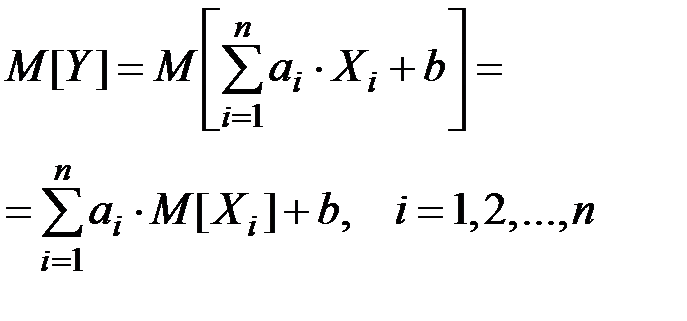 (П2.63)
(П2.63)
Теорема умножения математических ожиданий.
Математическое ожидание произведения двух коррелированных случайных величин X, Y выражается формулой:
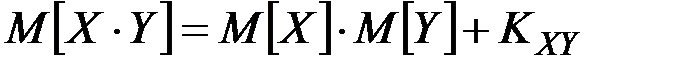 , (П2.64)
, (П2.64)
где КXY –– корреляционный момент величин X, Y.
Эту формулу можно записать в ином виде:
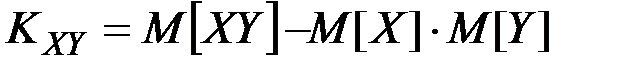 (П2.65)
(П2.65)
Математическое ожидание произведения двух некоррелированных случайных величин Х, Y равно произведению их математических ожиданий:
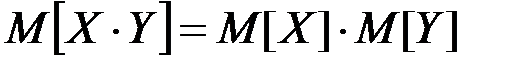 (П2.66)
(П2.66)
Если X1, X2, …, Xn –– независимые случайные величины, то математическое ожидание их произведения равно произведению их математических ожиданий:
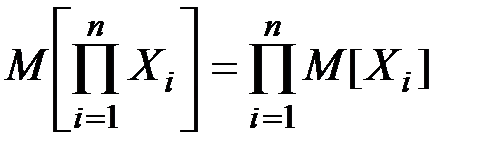 (П2.67)
(П2.67)
Дисперсия суммы двух случайных величин выражается формулой:
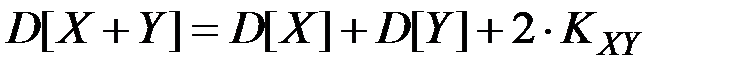 (П2.68)
(П2.68)
Дисперсия суммы нескольких случайных величин выражается формулой:
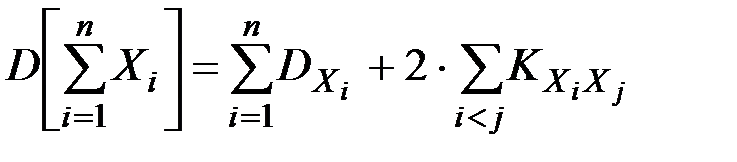 (П2.69)
(П2.69)
где Кxy –– корреляционный момент случайных величин Xi, Xj.
Дисперсия суммы некоррелированных случайных величин Xi равна сумме их дисперсий:
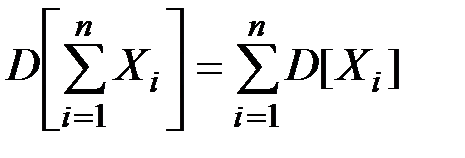 (П2.70)
(П2.70)
Дисперсия линейной функции нескольких случайных величин
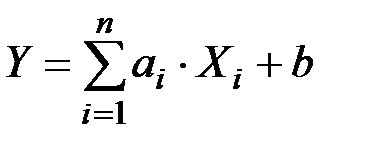
где аi , b –– не случайные величины, выражается формулой:
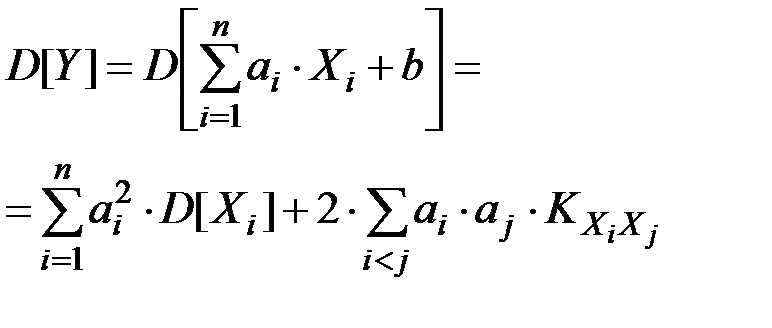 (П2.71)
(П2.71)
В случае, когда Х1 , Х2 , …, Хn не коррелированы,
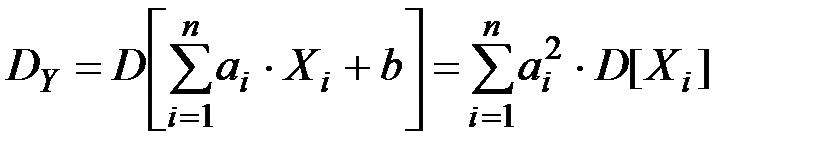 (П2.72)
(П2.72)
При сложении некоррелированных случайных векторов их корреляционные моменты складываются, т.е. если
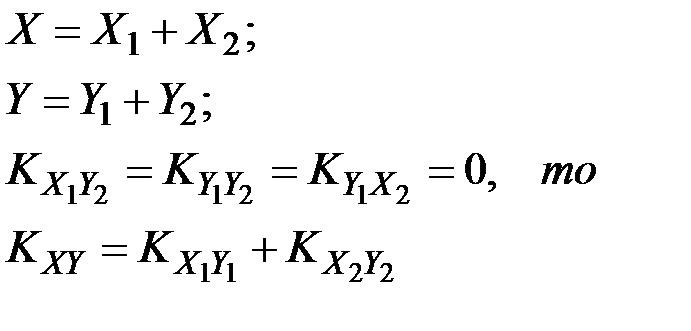 (П2.73)
(П2.73)
Задача П2.32.
Тело взвешивается на аналитических весах. Истинное (неизвестное нам) значение веса равно а. Вследствие ошибок результат каждого взвешивания случаен и взвешенное значение распределено по нормальному закону с параметрами а, s.
Для уменьшения ошибок пользуются следующим приемом: взвешивают тело n раз и в качестве приближенного значения веса берут среднее арифметическое:
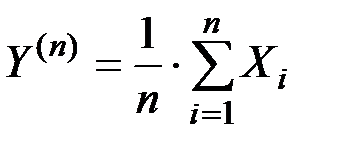
а) Найти характеристики случайной величины Y(n) (математическое ожидание и среднее квадратическое отклонение).
б) Сколько нужно сделать взвешиваний, чтобы уменьшить среднюю квадратическую ошибку веса в десять раз.
Решение[8]
а) 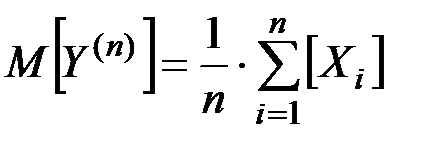
Поскольку все взвешивания производятся в одинаковых условиях, то
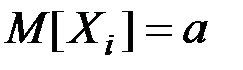 при любом i,
при любом i,
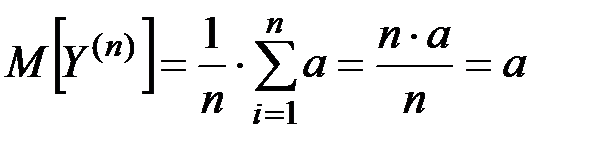
Считая ошибки отдельных взвешиваний независимыми, находим дисперсию величины Y(n) :
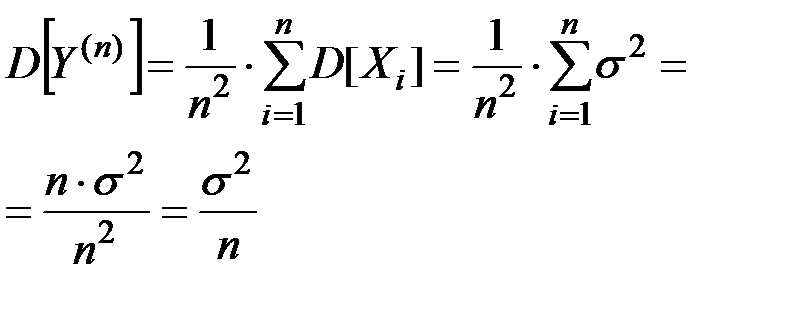
Число взвешиваний n находим из условия:
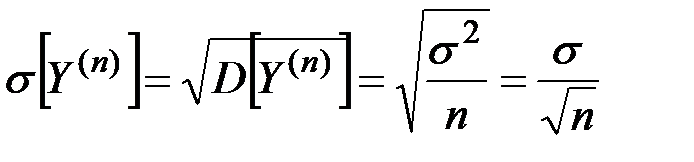
Для уменьшения среднеквадратической ошибки в десять раз необходимо выбрать значение n = 100 ( 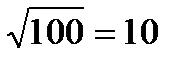 ).
).
Задача П2.33.
При работе прибора возникают случайные неисправности. Среднее число неисправностей, возникающих в единицу времени работы прибора, равно l. Число неисправностей за время t работы прибора –– случайная величина, распределенная по закону Пуассона с параметром а=l×t. Для ликвидации возникшей неисправности (ремонта) требуется случайное время Трем . Это время ремонта распределено по показательному закону:
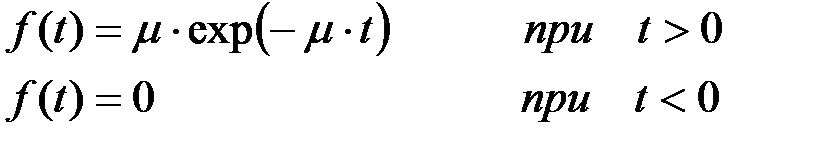
Времена устранения неисправностей неизвестны.
Найти:
а) среднюю долю времени, которую прибор будет исправно работать, и среднюю долю времени, которую он будет находиться в ремонте;
б) средний интервал времени между двумя последовательными неисправностями.
Решение.
Среднее время исправной работы (математическое ожидание времени, которое проработает прибор после пуска до остановки для ремонта) равно:
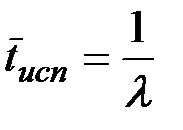
Среднее время ремонта:
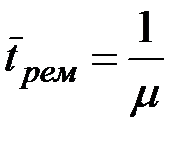
Средняя доля a времени, которую прибор будет работать исправно:
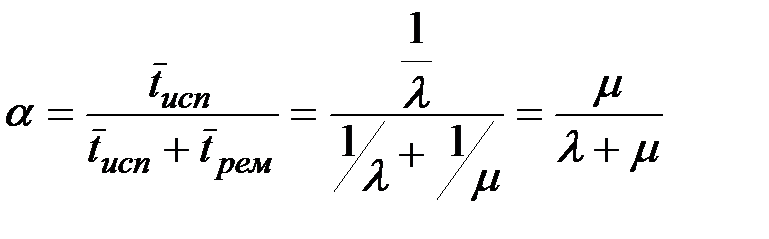
Средняя доля b времени, которую прибор будет находиться в ремонте:
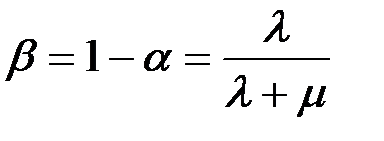
Средний интервал времени  между двумя последовательными неисправностями определяется по теореме сложения математических ожиданий (математическое ожидание суммы случайных величин равно сумме их математических ожиданий):
между двумя последовательными неисправностями определяется по теореме сложения математических ожиданий (математическое ожидание суммы случайных величин равно сумме их математических ожиданий):
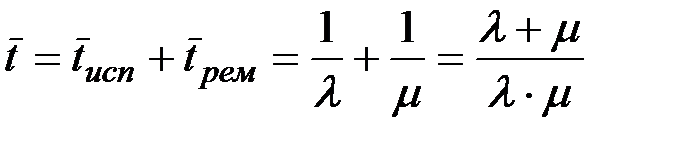
Задача П2.34.
В партии выпущенных изделий оказались смешанными а исправных и в неисправных изделий. Со склада без дополнительной проверки выбирается (берется сразу) k £ (a + b) изделий.
Определить математическое ожидание и дисперсию числа исправных изделий в составе выбранной партии.
Решение.
Пусть Х –– число выбранных исправных изделий
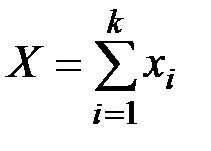 ,
,
где xi –– число исправных изделий, появившихся при i-м изъятии со склада.
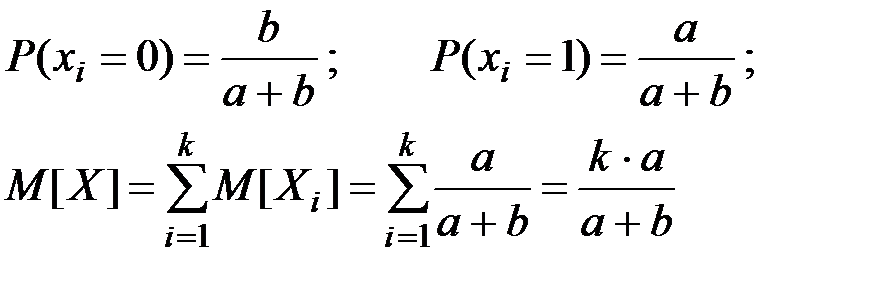
Для нахождения дисперсии D[X] найдем выражения для D[Xi ] и Kxi,
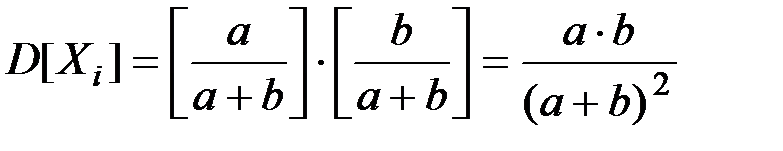
Напомним основные соотношения:
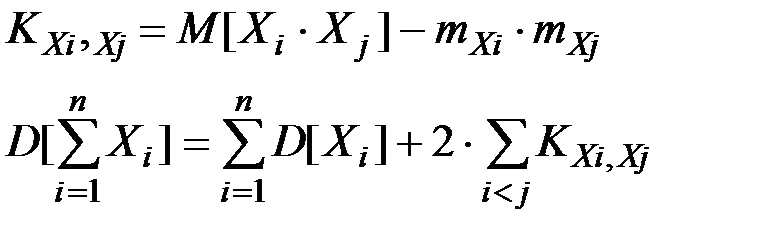
Построим таблицу распределения вероятностей для пары случайных величин Xi , Xj .
| Xj Xi | ||
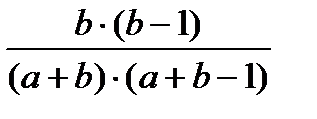
| 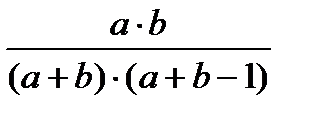
| |
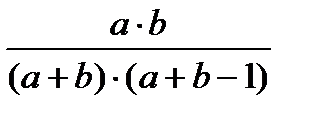
| 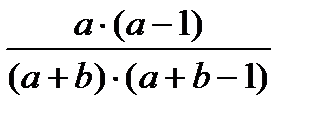
|
Имеем:
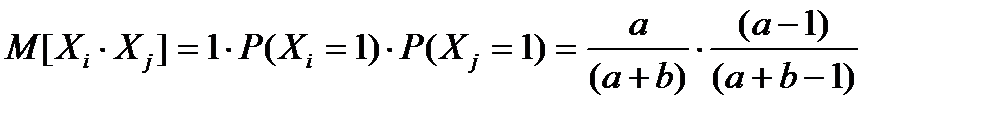
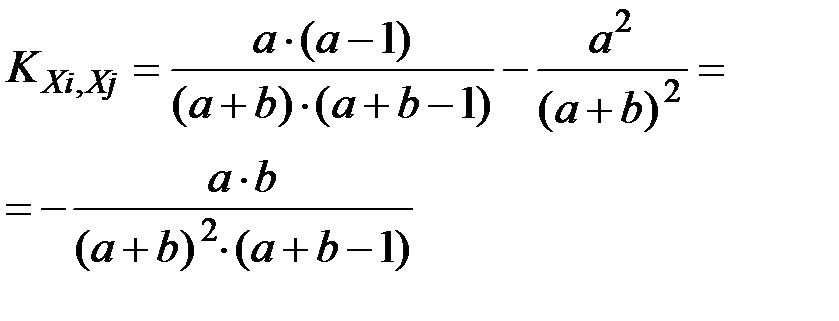
Далее можно найти дисперсию случайной величины Х:
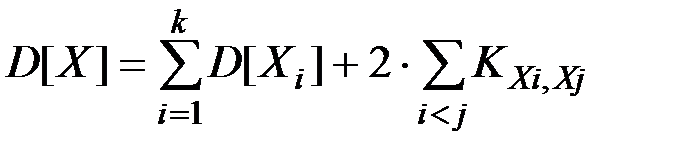
Поскольку дисперсии D[Xi] и корреляционные моменты KXi,Xj все одинаковы, то:
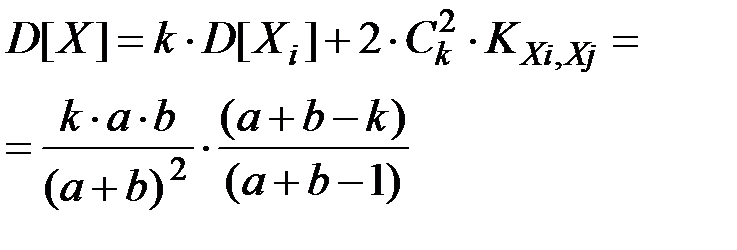
В частном случае, когда выбираются все изделия (k = a + b), получим естественный результат:
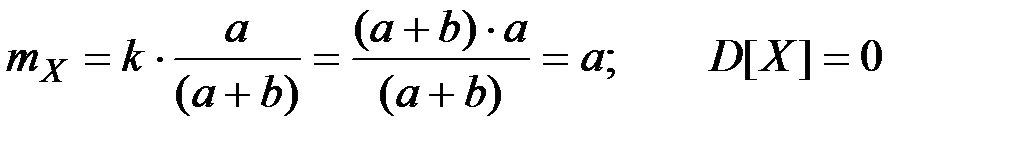 .
.
Задача П2.35.
Техническое устройство состоит из n узлов. Каждый узел может выходить из строя независимо от других. Узлы выходят из строя только последовательно, по одному. Время исправной работы i-го узла распределено по показательному закону с параметром li :
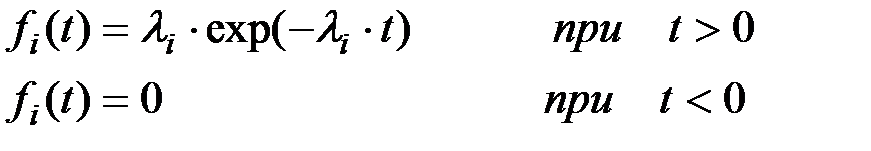
Каждый узел, оказавшийся неисправным, немедленно заменяется новым и поступает в ремонт. Ремонт узлов производится последовательно, по одному. Ремонт i-го узла продолжается случайное время, распределенное по показательному закону с параметром mi:
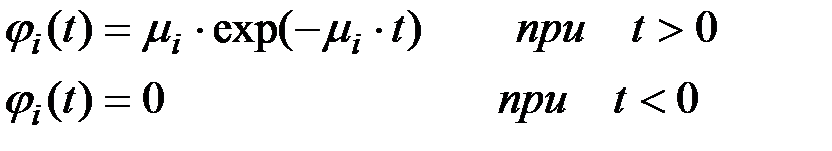
Устройство работает в течение времени t.
Требуется определить:
а. Математическое ожидание и дисперсию числа узлов, подлежащих замене.
б. Математическое ожидание суммарного времени Т, которое будет затрачено на ремонт вышедших из строя узлов.
Решение[8]
а. Обозначим через Xi число узлов i-го типа, вышедших из строя за время t. Очевидно, что эта случайная величина распределена по закону Пуассона и имеет:
математическое ожидание 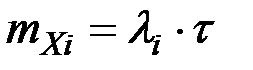
дисперсию 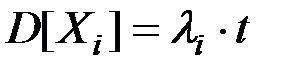 .
.
Обозначим через Х общее число узлов, вышедших из строя за время t. Тогда имеем:
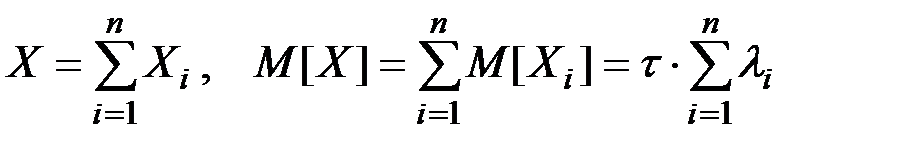
Поскольку величины Хi независимы, то:
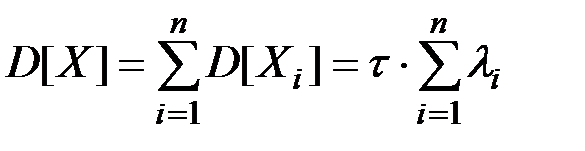
б. Обозначим через Тi общее время, затраченное на ремонт всех вышедших из строя за время t узлов i-го типа. Оно представляет собой сумму времен, затраченных на ремонт каждого из узлов. Поскольку число вышедших из строя узлов i-го типа равно Xi , имеем:
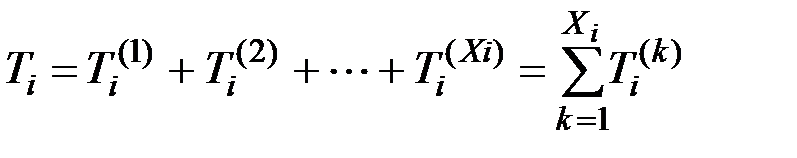 ,
,
где 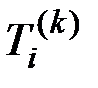 –– случайная величина, распределенная по показательному закону с параметром mi.
–– случайная величина, распределенная по показательному закону с параметром mi.
Величины 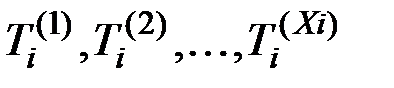 –– независимы.
–– независимы.
Найдем математическое ожидание величины Тi. Для этого вначале предположим, что случайная величина Xi приняла определенной значение, тогда:

Умножив это условноематематическое ожидание на вероятность Pm того, что случайная величина Xi приняла значение m, и просуммировав все эти произведения, мы найдем полное (безусловное) математическое ожидание величины Тi:
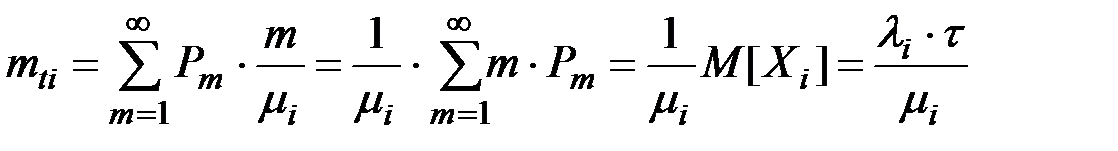
Применяя далее теорему сложения математических ожиданий, получим:
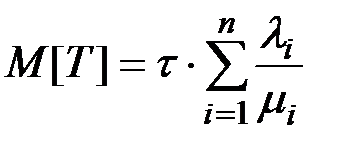
Замечание.
Тот же результат можно получить путем следующих (не вполне строгих) рассуждений. Среднее число выходов из строя узлов i-го типа за время t равно li×t. Среднее время ремонта одного узла i-го типа равно 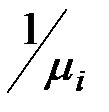 , а среднее время, которое будет затрачено на ремонт всех вышедших за время t узлов i-го типа равно
, а среднее время, которое будет затрачено на ремонт всех вышедших за время t узлов i-го типа равно 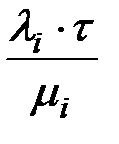 .
.
Тогда среднее время, которое будет затрачено на ремонт узлов всех типов будет равно:
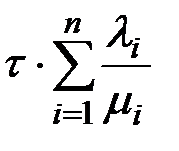 .
.
Заключение
Настоящее пособие составлено по материалам последних публикаций по теории надежности технических систем, в прикладном ее аспекте.
В отличие от предыдущего издания (2010 г.) в пособии исключены материалы, не вошедшие в курс лекций ни на факультете безопасности, ни на инженерно-строительном факультете Санкт-Петербургского государственного политехнического университета. Сокращено число задач, относящихся к проверке знаний по теории вероятностей, исключены задачи, связанные с расчетами параметров случайных функций.
Вместе с тем в пособие добавлен раздел логико-вероятностных методов оценки надежности, без которых определение надежности систем сложных структур было бы весьма затруднительной, добавлены расчетные примеры оценки надежностной и структурной значимости элементов, входящих в состав сложных систем, изменена структура пособия, добавлен раздел оценки риска и влияния надежности системы на безопасность.
Решение многих примеров изменено с целью использования современных вычислительных средств персональных компьютеров, с помощью Mathcad, Matlab.
Перечисленные выше изменения проведены с целью адаптации пособия к современным вычислительным средствам и приближения теории надежности технических систем к практическим задачам.
Литература
1. Куличкин Ю.В., Яковлев В.В. Практические рекомендации по применению надежности технических систем. СПб, ВВМ, 2010, 208с.
2. Яковлев В.В. Прикладные аспекты надежности технических систем. СПбГПУ, 2000, 178с.
3. Чусов А.Н., Яковлев В.В. Управление безопасностью природно-технических систем. СПбГПУ, 2011, 227с.
4. Приказ Ростехнадзора от 11.04.2016г. №144. Методическое руководство по проведению анализа опасности и оценки риска аварий на опасных производственных объектах.
5. Приказ Ростехнадзора от 13.05.2015г. №188. Методическое руководство по проведению анализа опасности и оценки риска аварий на опасных производственных объектах.
6. Закон РФ от 22.07.2008 123-ФЗ «Технический регламент о требованиях пожарной безопасности».
7. Федоров М.П., Чусов А.Н., Яковлев В.В. Модели управления безопасностью природно-технических систем. СПбГПУ, 2011, 261с.
8. Вентцель Е.С., Овчаров Л.А. Теория вероятностей. «Наука», М.: 1973 г., 364с.
9. Потемкин В.Г. Введение в MATLAB.Диалог-Мифи, М.:200, 247с.
10. Мещеряков В.В. Задачи по статистике и регрессионному анализу с MATLAB. Диалог-Мифи, М.: 2009448с.
11. Поршнев С.В., Беленкова И.В. Численные методы на базе MATHCAD, СПб, «БХВ-Петербург», 2005, 450с.
12. Рябинин И.А. Надежность и безопасность структурно-сложных систем.СПб, 2000, 248с.
13. Гаенко В.П. Безопасность технических систем. СПб, «СВЕН», 2014, 167с.
14. Малкин В.С. надежность технических систем и техногенный риск. Ростов – на- Дону. Феникс, 2010, 429с.
15. Яковлев В.В. Риск в природно-технической среде. СПбГПУ, 2015, 508с.
16. Кетков Ю., Кетков А., Шульц М. Matlab 6.х: программирование численных методов.СПб «БХВ», 2004, 662с.
17. Гук Ю.Б., Карпов В.В. Теория надежности в электроэнергетике. СПбГПУ, 1999, 81с.
18. Ануфриев И.Е. Информатика. Пакет Matlab. СПбГПУ, 2010, 65с.
| S1 |
| λ21 |
| S2 |
| S3 |
| S4 |
| λ31 |
| λ23 |
| λ12 |
| λ13 |
| S0 |
| S1 |
| S2 |
| S0 |
| S1 |
| S2 |
| λ20 |
| S0 |
| S2 |
| S1 |
| λ12 |
| λ01 |
| t |
|
|
| t0 |
| t1 |
| t0 |
| t |
| t1=t0 = |
| II |
| I |
| У0 |
| У1 |
| У2 |
| У3 |
| S03 |
| S02 |
| S01 |
| S00 |
| S13 |
| S12 |
| S11 |
| S10 |
| 3l1 |
| 2l1 |
| l1 |
| l0 |
| l0 |
| l0 |
| l0 |
|
|
|
| t0 |
| λP |
| λA |
| λ |
| t |
| τ |
| A |
| Б |
| А (гипотеза «а») |
| (гипотеза «б») |
| А |
| Б |
| t |
| T |
| ti+1 |
| a(t) |
| ti |
| ∆τi |
| t |
| l0 |
| l0 |
| lк |
| l0 |
| lк |
| lк |
| l0 |
| l0 |
| lк |
| l0 |
| lк |
| t |
| λ |
| S0 |
| S1 |
| μ |
| S0 |
| S1 |
| λ |
| S0 |
| S1 |
| (m+1)·λ |
| μ |
| λ |
| (m-k)λ |
| (m-k+1)λ |
| (m-1)λ |
| (k+1)μ |
| 2μ |
| S0 |
| S1 |
| Sk |
| Sm |
| mλ |
| μ |
| kμ |
| mμ |
| λ |
| S0 |
| S1 |
| μ |
| p |
| p |
| p |
| p |
| p1 |
| p |
| p3 |
| p4 |
| p1 |
| p1 |
| p5 |
| p5 |
| p2 |
| p2 |
| p2 |
| 1.0 |
| F(x) |
| 0.216 |
| 0.648 |
| 0.936 |
| X |
Дата добавления: 2019-02-07; просмотров: 1698;
