П2.4. Повторение опытов.
Частная теорема о повторении опытов.
Если производится n независимых опытов в одинаковых условиях, причем в каждом из них событие А появляется с вероятностью р, то вероятность 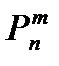 того, что событие А реализуется в этих n опытах ровно m раз, выражается биномиальным распределением вероятностей:
того, что событие А реализуется в этих n опытах ровно m раз, выражается биномиальным распределением вероятностей:
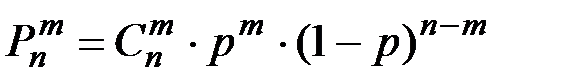 (П2.14)
(П2.14)
где 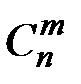 - число сочетаний из n элементов по m.
- число сочетаний из n элементов по m.
Часто можно встретить эту формулу с использованием равенства  .
.
Вероятность того, что в этих n опытах событие А произойдет хотя бы один раз определяется формулой:
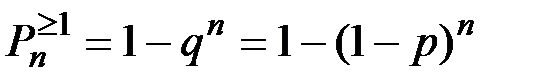 (П2.15)
(П2.15)
Общая теорема о повторении опытов.
Если производится n независимых опытов в различных условиях, причем вероятность события А в i–м опыте равна pi (i=1,2,…,n), то вероятность 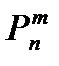 того, что событие А появится в этих опытах ровно m раз, равна коэффициенту при zm в разложении по степеням z производящей функции:
того, что событие А появится в этих опытах ровно m раз, равна коэффициенту при zm в разложении по степеням z производящей функции:
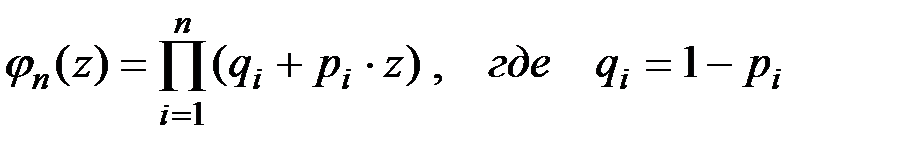 (П2.16)
(П2.16)
Вероятность хотя бы одного появления события А при n независимых опытах в различных условиях равна:
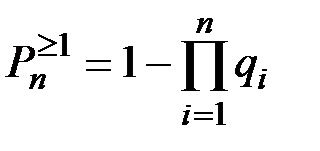 (П2.17)
(П2.17)
Для любых условий (одинаковых и различных) выполняется условие:
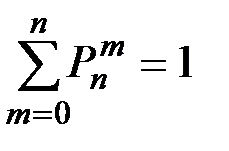 (П2.18)
(П2.18)
Вероятность 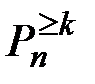 того, что при n опытах событие А появится не менее k раз, выражается формулой:
того, что при n опытах событие А появится не менее k раз, выражается формулой:
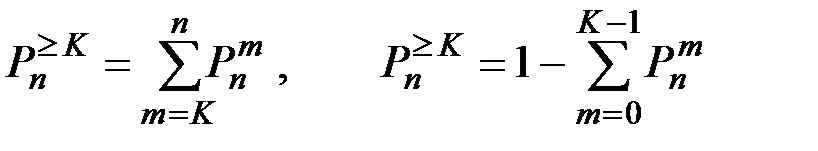 (П2.19)
(П2.19)
где 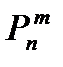 определяется по формуле (П2.14).
определяется по формуле (П2.14).
Задача П2.23.
Прибор состоит из 10 узлов. Надежность (вероятность безотказной работы в течение времени t) для каждого узла одинакова и равна р. Узлы выходят из строя независимо один от другого.
Найти вероятность того, что за время t :
а) не откажет хотя бы один узел;
в) не откажет ровно один узел;
с) не откажет ровно два узла;
d) не откажет не менее двух узлов.
Решение [8]
а) 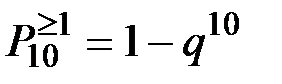
в) 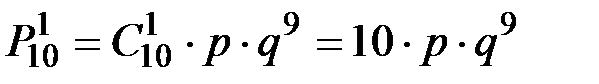
с) 
d) 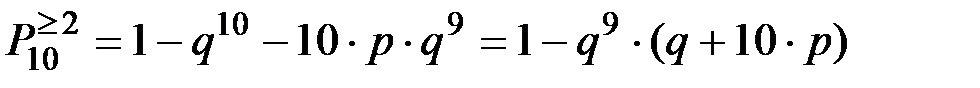
Задача П2.24.
Завод изготавливает изделия, каждое из которых с вероятностью r (независимо от других) оказывается дефектным. При осмотре изделия дефект, если он имеется, обнаруживается с вероятностью р. Для контроля из продукции завода выбирается n изделий.
Определить вероятности реализации следующих событий:
А –– ни в одном изделии не будет обнаружен дефект;
В –– среди n изделий ровно в двух будет обнаружен дефект;
С - среди n изделий не менее чем в двух будет обнаружен дефект.
Решение [8]
Вероятность того, что в одном наугад выбранном изделии будет обнаружен дефект равна произведению (p×r), тогда:
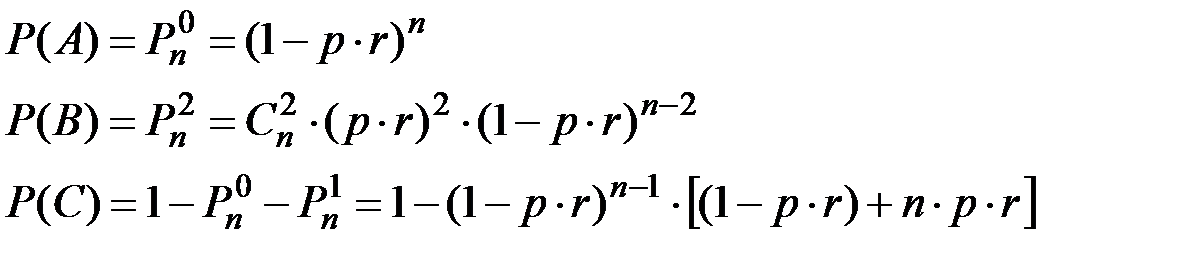
Задача П2.25.
В течение времени t эксплуатируется N приборов. Каждый прибор имеет надежность р и выходит из строя независимо от других. Найти вероятность Р(А) того, что мастер, вызванный по окончании времени t для ремонта неисправных приборов, не справится со своей задачей за время t, если на ремонт каждого прибора мастеру требуется время t0.
Решение.

Случайные величины. Законы распределения. Числовые характеристики случайных величин.
Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.
Функцией распределения случайной величины X называется функция F(x), выражающая вероятность того, что случайная величина X примет значение меньше, чем константа x:
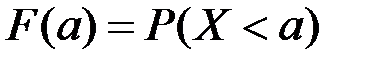 (П2.20)
(П2.20)
Функция F (x) есть неубывающая функция, F ( - ¥ ) = 0, F ( + ¥ ) = 1.
Плотностью распределения случайной величины называется функция
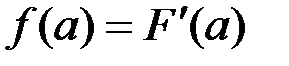 (П2.21)
(П2.21)
Плотность распределения любой случайной величины неотрицательна:
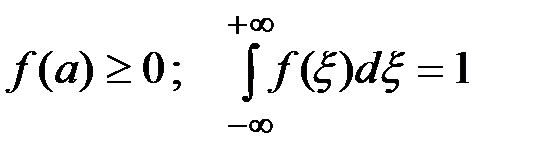 (П2.22)
(П2.22)
График плотности f(а) называется кривой распределения.
Элементом вероятности для случайной величины X называется величина f(а)dа, приближенно выражающая вероятность попадания случайной точки X в элементарный отрезок dа, примыкающий к этой точке.
Функция распределения случайной величины F(а) выражается через плотность распределения формулой:
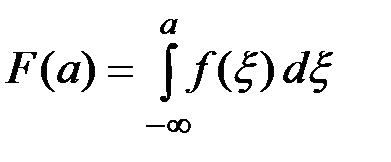 (П2.23)
(П2.23)
Вероятность W попадания случайной величины X на участок, протяженностью от a до b, включая a, выражается формулой:
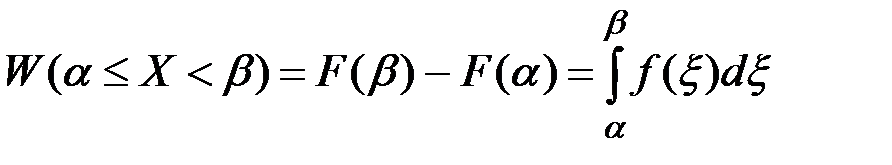 (П2.24)
(П2.24)
Математическим ожиданием случайной величины X называется ее среднее значение, вычисляемое по формулам:
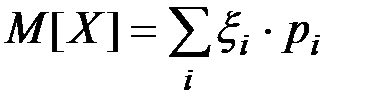 (П2.25)
(П2.25)
для дискретных случайных величин,
где xi –– значение случайной величины,
рi –– вероятность реализации значения xI .
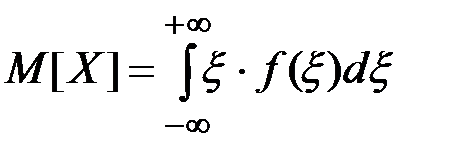 (П2.26)
(П2.26)
для непрерывных случайных величин
Дисперсией случайной величины называется математическое ожидание квадрата соответствующей центрированной случайной величины.
Для дискретных случайных величин:
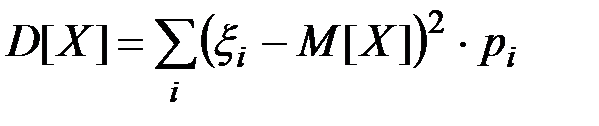 (П2.27)
(П2.27)
Для непрерывных случайных величин:
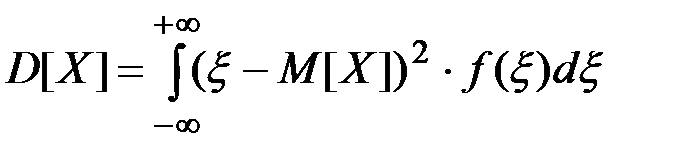 (П2.28)
(П2.28)
Средним квадратическим отклонением случайной величины X называется корень квадратный из дисперсии
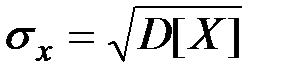 (П2.29)
(П2.29)
Центрированной случайной величиной 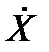 называется разность между случайной величиной Х и ее математическим ожиданием mx:
называется разность между случайной величиной Х и ее математическим ожиданием mx:
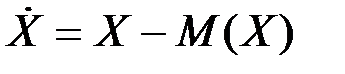 (П2.30)
(П2.30)
Начальным моментом k-го порядка случайной величины Х называется математическое ожидание k-й степени этой случайной величины:
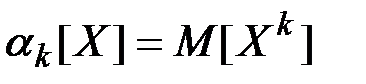 (П2.31)
(П2.31)
Центральным моментом k-го порядка случайной величины Х называется математическое ожидание k-й степени центрированной случайной величины:
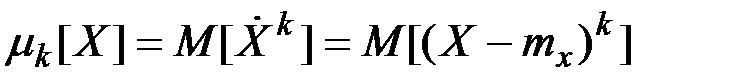 (П2.32)
(П2.32)
Биномиальный закон распределения числа n появления события A в n независимых опытах.
Дискретная случайная величина X называется распределенной по биномиальному закону, если она может принимать значения 0,1,2,…n, а вероятность того, что X = m < n выражается формулой:
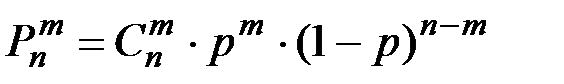 (П2.33)
(П2.33)
где 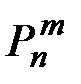 –– вероятность появления m событий при проведении n испытаний,
–– вероятность появления m событий при проведении n испытаний,
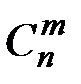 –– число сочетаний из n по m,
–– число сочетаний из n по m,
p –– вероятность появления события А в одном испытании;
q = 1-p –– вероятность непоявления события А.
Биномиальное распределение отличается следующими свойствами:
математическое ожидание числа событий (при проведении n испытаний) равно М[X] = n×p;
среднеквадратическое отклонение
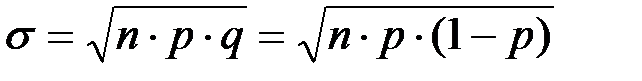 (П2.34)
(П2.34)
При увеличении числа испытаний биномиальное распределение приближается к нормальному со средним значением:
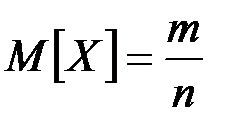 (П2.35)
(П2.35)
и дисперсией
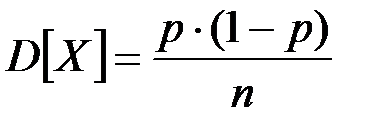 (П2.36)
(П2.36)
Закон Пуассона.
Дискретная случайная величина X называется распределенной по закону Пуассона, если ее возможные значения 0, 1, 2,…, n,…, а вероятность того, что X=n выражается зависимостью:
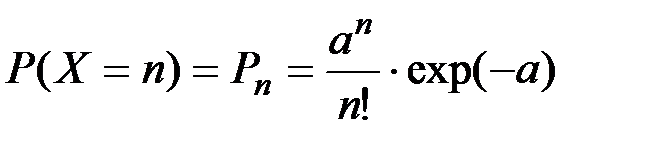 (П2.37)
(П2.37)
где a > 0 –– параметр закона Пуассона.
Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона, вычисляются по формулам:
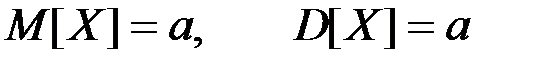 (П2.38)
(П2.38)
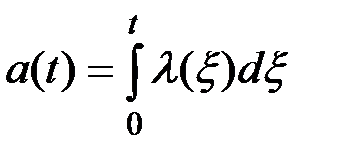 (П2.39)
(П2.39)
где l(x) –– функция интенсивности появления случайного события.
Вероятность числа n реализаций за время t случайных событий, распределенных по закону Пуассона, при l(t) = const = l вычисляется по формуле:
 (П2.40)
(П2.40)
где l –– интенсивность появления случайного события, равная среднему числу реализации событий в единицу времени;
l×t = а –– среднее число событий, реализовавшихся за время t.
Характерным признаком распределения Пуассона является равенство математического ожидания и дисперсии
(М[X] = l×t, D[X] = l×t).
Функция вида:
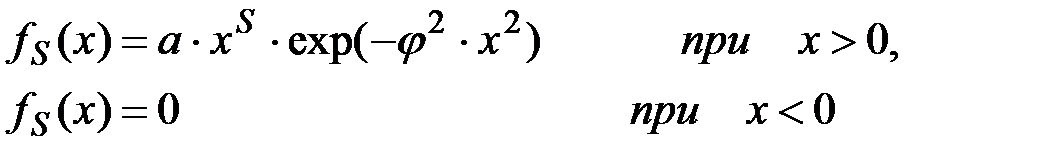 (П2.41)
(П2.41)
где a>0, j>0 –– некоторые постоянные,
S –– натуральное число
обладает свойствами плотности распределения. Некоторые из законов распределения случайных величин типа fS(x) имеют определенные названия, например:
f1(x) –– называется законом Релея,
f2(x) –– называется законом Максвелла.
Для закона Релея:
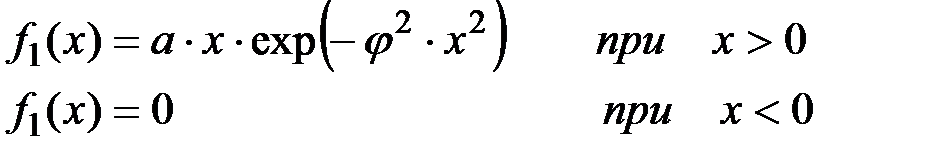 (П2.42)
(П2.42)
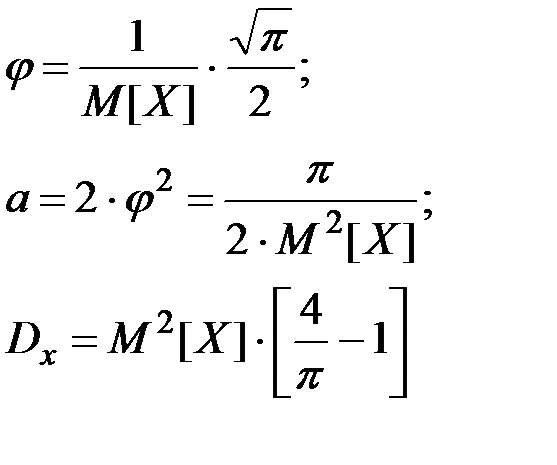 (П2.43)
(П2.43)
Для закона Максвелла:
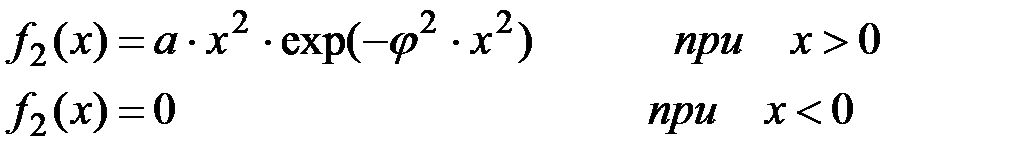 (П2.44)
(П2.44)
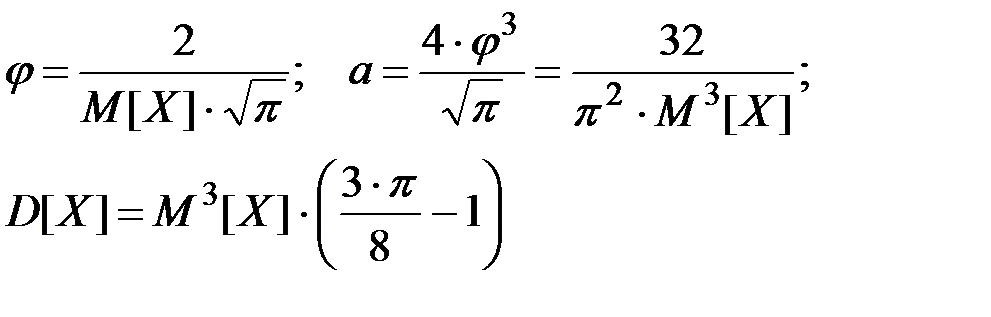 (П2.45)
(П2.45)
Все законы вида:
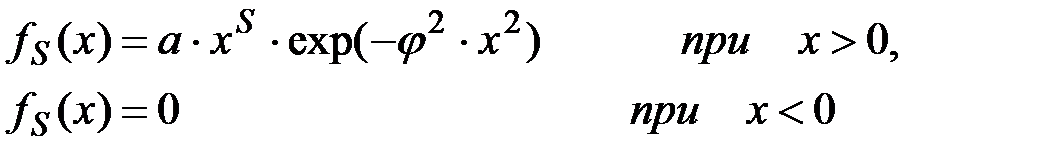 (П2.46)
(П2.46)
являются однопараметрическими, т.е. зависят только от одного параметра, в качестве которого можно задать, например, математическое ожидание или дисперсию.
Равномерный закон распределения непрерывной случайной величины.
Непрерывная случайная величина X называется равномерно распределенной в интервале ( a, b ), если ее плотность распределения на этом интервале постоянна:
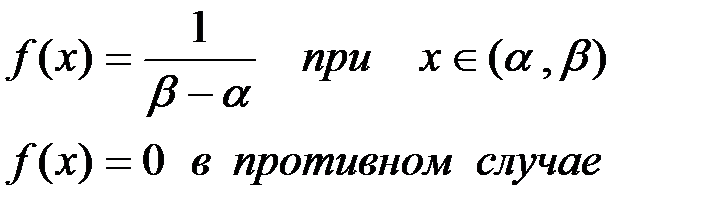 (П2.47)
(П2.47)
Математическое ожидание и дисперсия случайной величины при ее равномерном распределении соответственно равны:
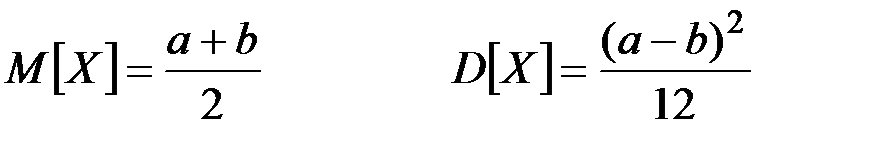 (П2.48)
(П2.48)
Вывод формулы (2.48).
По определению:
дисперсия 
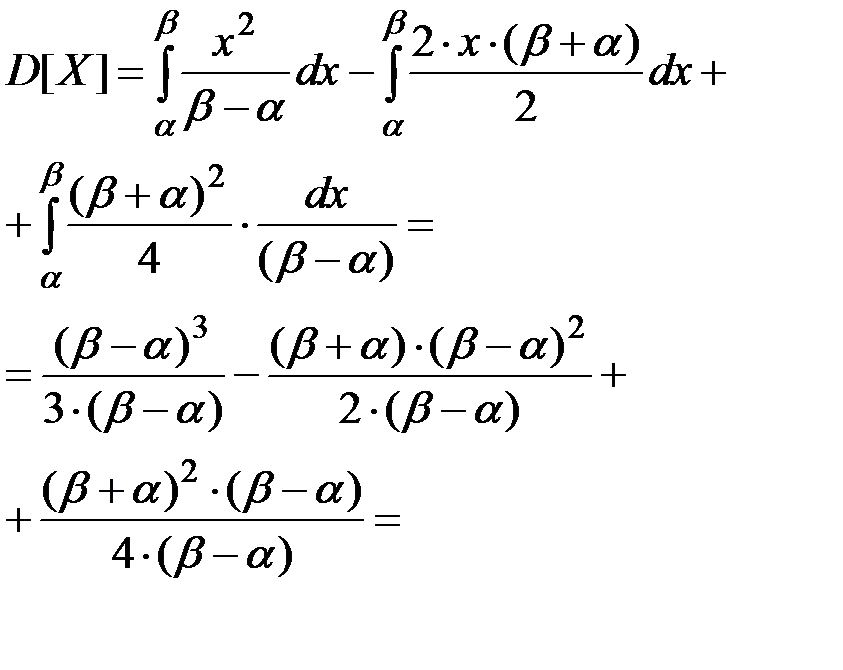
Поскольку случайная величина распределена равномерно на интервале (a, b), то:
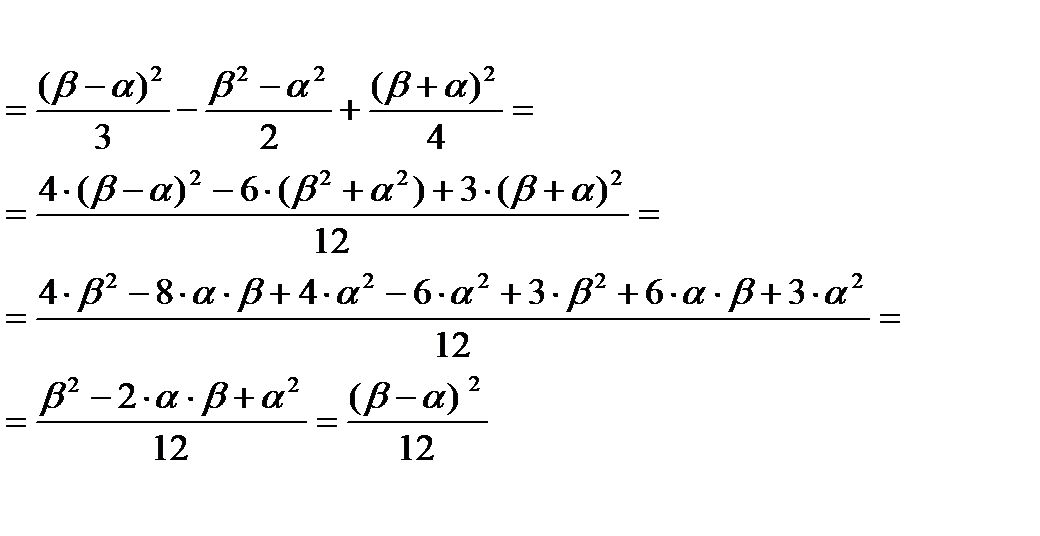
Нормальный закон распределения случайных величин.
Непрерывная случайная величина X называется распределенной по нормальному закону, если плотность ее распределения подчинена зависимости:
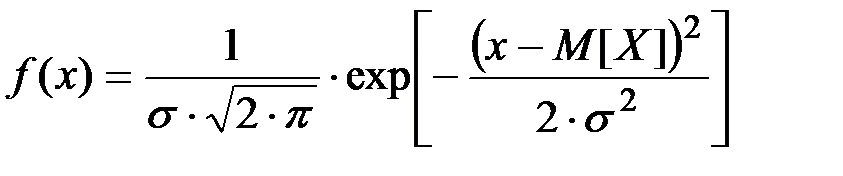 (П2.49)
(П2.49)
где: m –– математическое ожидание случайной величины;
D = s2 –– ее дисперсия.
Вероятность попадания случайной величины X , распределенной по нормальному закону, в интервале (a, b) выражается формулой:
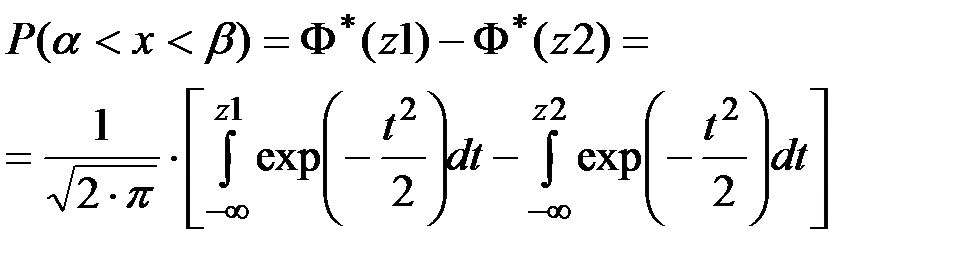 (П2.50)
(П2.50)
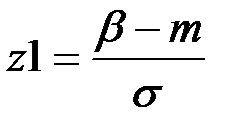 (П2.51)
(П2.51)
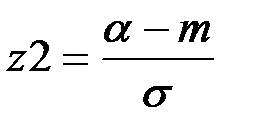 (П2.52)
(П2.52)
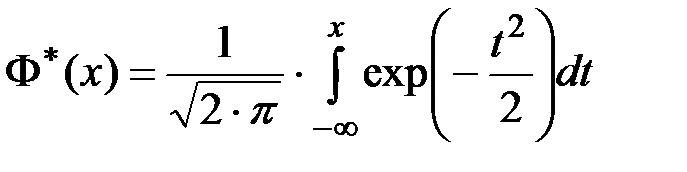 (П2.53)
(П2.53)
Функция Ф*(x) –– табулированная функция Лапласа.
На практике бывает удобнее пользоваться аппроксимацией координатного закона поражения Ф.А. Евстифеевым.
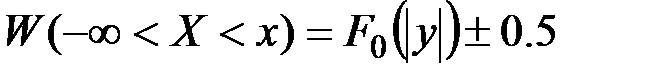 (П2.54)
(П2.54)
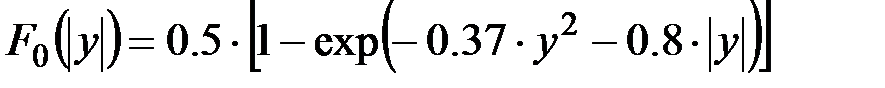 (П2.55)
(П2.55)
где 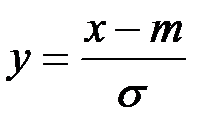 –– нормированное отклонение случайной величины Х.
–– нормированное отклонение случайной величины Х.
В (2.54) принимается знак (-), если величина «y» отрицательна и (+) в противном случае.
Распределение Вейбулла.
Плотность распределения:
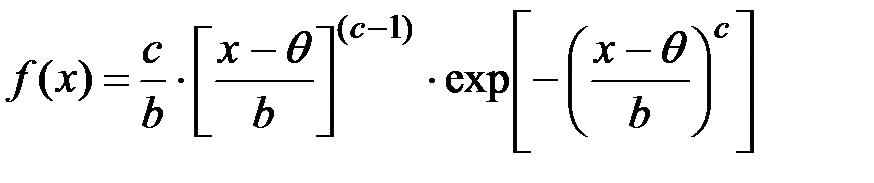 (П2.56)
(П2.56)
где 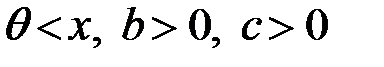
Функция распределения (функция отказов или ненадежности):
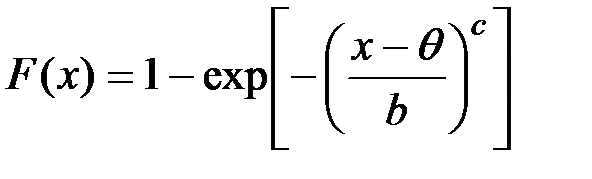 (П2.57)
(П2.57)
Функция надежности:
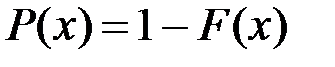
Интенсивность отказов:
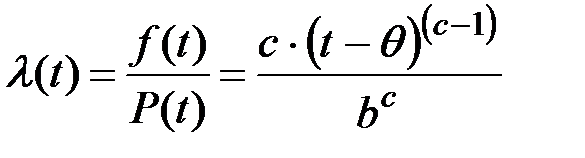 (П2.58)
(П2.58)
Для начального этапа эксплуатации технических систем распределение Вейбулла используется для расчета вероятности безотказной работы системы в течение времени t. Для этих целей можно принять значения:
q = 0, b ³ 1, c @ 0.5, tÎ[0, t1]
где t1 –– окончание этапа приработки технической системы.
Ниже приведен пример изменения интенсивности отказов (рис. П2.1), подчиненных распределению Вейбулла с определенными выше значениями констант.

Рис. П2.1. Изменение интенсивности отказов на начальном этапе эксплуатации системы.
Задача П2.26.
Производится три независимых испытаний приборов, в каждом из которых неисправность (событие А) появляется с вероятностью 0.4. Рассматривается случайная величина Х –– число выявленных неисправностей в трех опытах.
Необходимо построить ряд распределения и функцию распределения случайной величины Х. Найти ее математическое ожидание M[X], дисперсию D[X], среднее квадратическое отклонение sх и третий центральный момент m3[X].
Решение [8].
Введем обозначения:
xi –– число неисправностей, обнаруженных в трех испытаниях;
pi –– вероятность того, что в результате трех испытаний будет обнаружено ровно xi неисправностей.
Эта вероятность рассчитывается по формуле (П2.33) биномиального закона распределения дискретных случайных величин. Тогда ряд распределения дискретной случайной величины и функция распределения имеют вид:
| xi | ||||
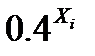
| 0.4 | 0.16 | 0.064 | |
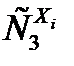
| ||||

| 0.216 | 0.36 | 0.6 | |
| pi | 0.216 | 0.432 | 0.288 | 0.064 |
| F(x) | 0+0.216=0.216 | 0.216+0.432= 0.648 | 0.648+0.288= 0.936 |
Математическое ожидание
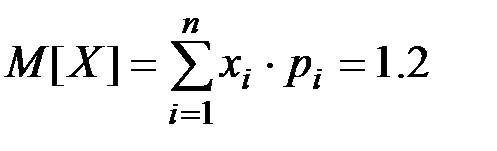
Дисперсия
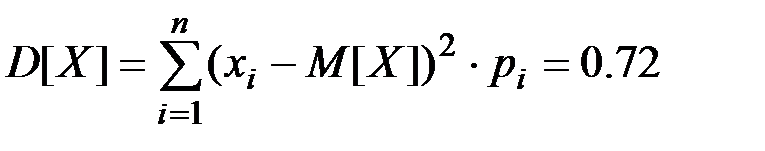 ;
;
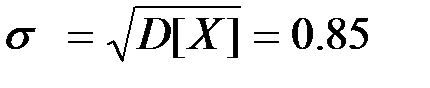
Третий центральный момент
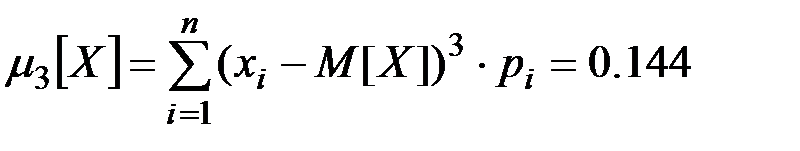
Задача П2.27.
Производится n независимых опытов, в каждом из которых с вероятностью р появляется событие А. Рассматривается случайная величина l –– частота появления события А в n опытах, т.е. отношение числа появления события А к общему числу n произведенных опытов.
Найти ряд распределения случайной величины l, найти ее математическое ожидание, дисперсию.
Решение.
Пусть q = 1 - p;
Тогда M[l]= p; 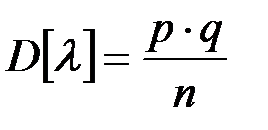 ,
,
Ряд распределения случайной величины имеет вид:
| l | 1/n | … | m/n | … | ||
| pl | qn | 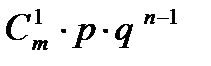
| … | 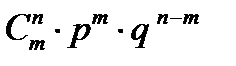
| … | pn |
Задача П2.28.
При работе ЭВМ иногда возникают сбои. Поток сбоев можно считать простейшим. Среднее число сбоев за сутки равно 1.5.
Определить вероятности следующих событий:
А –– за двое суток не произойдет ни одного сбоя;
В –– в течение суток произойдет хотя бы один сбой;
С –– за неделю (7 суток) работы ЭВМ произойдет не менее трех сбоев.
Решение.
Вероятность возникновения N сбоев за время Т определяется по закону Пуассона выражением:
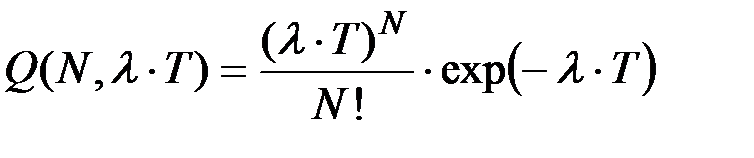
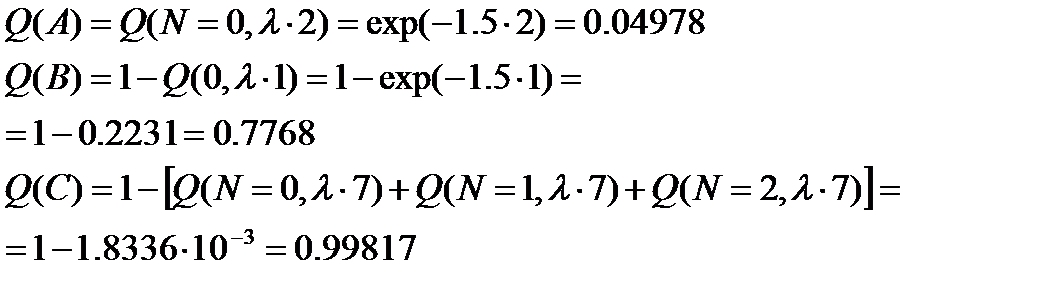
Задача П2.29.
Электронная лампа работает исправно в течение случайного значения времени Т, распределенного по показательному закону:
f(t) = 0 при t < 0
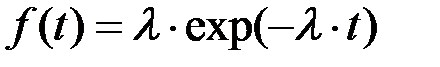 при t > 0.
при t > 0.
По истечении времени Т лампа выходит из строя, после чего она немедленно заменяется на новую.
Определить вероятности того, что за время t
лампу придется менять не менее трех раз.
Решение.
Отказы ламп образуют простейший поток с плотностью l. Математическое ожидание числа отказов а за время t равно 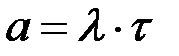 .
.
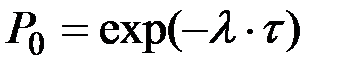 ,
,
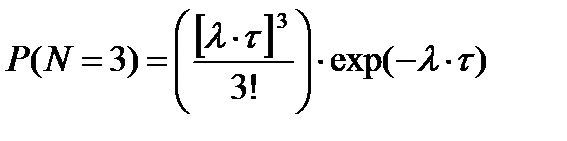 ,
,
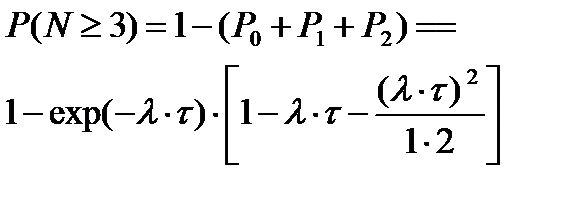
Задача П2.30.
Техническое устройство состоит из трех узлов. В первом узле работает n1 элементов, во втором –– n2, в третьем –– n3.
Первый узел безусловно необходим для работы устройства, второй и третий –– дублируют друг друга. Время работы каждого элемента распределено по показательному закону. Среднее время работы элемента, входящего в первый узел равно 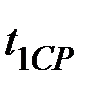 ,среднее время работы элементов, входящих во второй и третий узлы ––
,среднее время работы элементов, входящих во второй и третий узлы –– 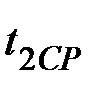 .
.
Первый узел выходит из строя, если в нем отказало не менее двух элементов, второй (третий) –– при выходе из строя хотя бы одного элемента.
Для выхода из строя устройства в целом достаточно, чтобы отказал первый узел или второй и третий вместе.
Найти вероятность того, что за время t техническое устройство выйдет из строя.
Решение.
Пусть Q –– вероятность выхода из строя устройства,
Q1 –– вероятность выхода из строя первого узла,
Q2 –– вероятность выхода из строя второго узла,
Q3 –– вероятность выхода из строя третьего узла;
q1, q2, q3 –– вероятности выхода из строя одного элемента соответствующего i-го узла.
Тогда вероятность выхода из строя устройства равна:
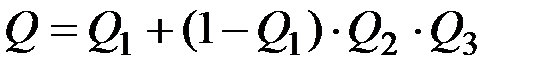
Вероятность выхода из строя первого узла за время t:
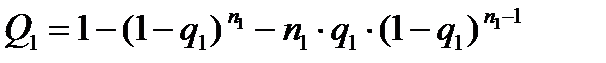
Вероятность выхода из строя одного элемента соответствующего узла за время t:
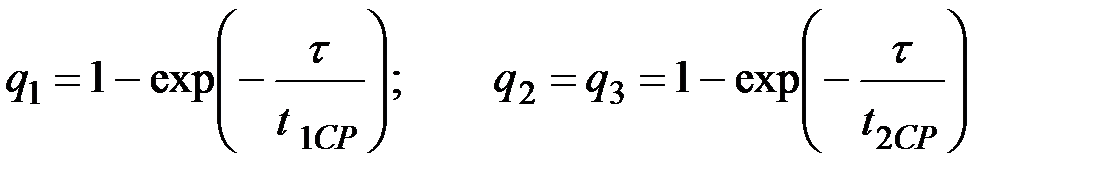
Вероятности Q2, Q3 выхода из строя второго и третьего узлов рассчитываются по формулам:
 .
.
Ниже приведено решение этой задачи в Matlab
T1cp=7000;T2cp=10000;T3cp=8000; n1=4;n2=2;n3=1; t=1000;
q1=1-exp(-t/T1cp); ненадежность одного элемента из первой группы
q2=1-exp(-t/T2cp); ); ненадежность одного элемента из второй группы
q3=1-exp(-t/T3cp); ); ненадежность одного элемента из третьей группы
Q2=1-(1-q2)^n2;вероятность отказа второго устройства
Q3=1-(1-q3)^n3; вероятность отказа третьего устройства
Q1=1-(1-q1)^n1-n1*q1*(1-q1)^(n1-1);вероятность отказа первого устройства
[Q1 Q2 Q3] вероятности отказов первого, второго и третьего устройств
QC=Q1+(Q1)*Q2*Q3вероятность отказа системы
ans =0.0884 0.1813 0.1175
QC = 0.0903
Задача П2.31[14].
Автомашина проходит технический осмотр и обслуживание. Число неисправностей, обнаруженных во время осмотра, распределено по закону Пуассона с параметром а. Если неисправность не обнаружена, осмотр машины продолжается в среднем 2 часа. Если обнаружены одна или две неисправности, то на устранение каждой из них тратится еще полчаса. Если обнаружено более двух неисправностей, машина ставится на ремонт, где она находится в среднем 4 часа.
Определить закон распределения среднего времени Т обслуживания и ремонта машины, определить его математическое ожидание.
Решение.
| Индекс i | ||||
| Число неисправностей | Более 2 х | |||
| Ti | 2.5 | |||
| pi | exp(-a) | 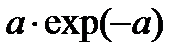
| 
| 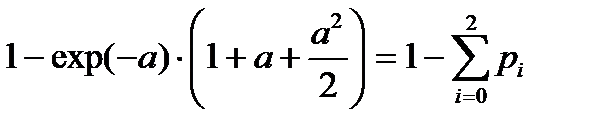
|
Математическое ожидание времени ремонта и обслуживания:
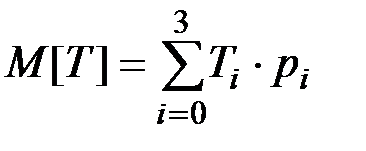
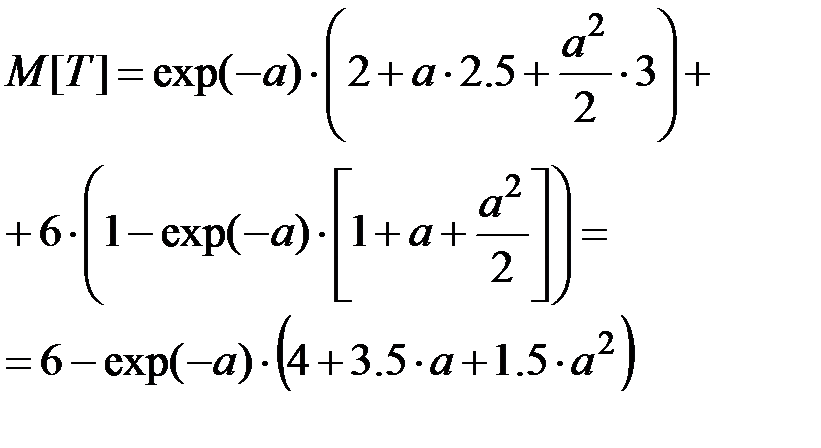
Числовые характеристики функций случайных величин.
Если Х –– дискретная случайная величина с рядом распределения
| xi | x1 | x2 | … | xn |
| pi | p1 | p2 | … | pn |
и величина Y связана с Х функциональной зависимостью 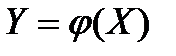 , то математическое ожидание случайной величины Y равно:
, то математическое ожидание случайной величины Y равно:
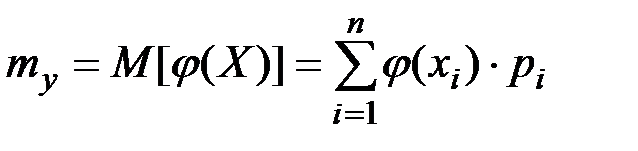 , (П2.59)
, (П2.59)
при этом дисперсия выражается любой из двух следующих формул:
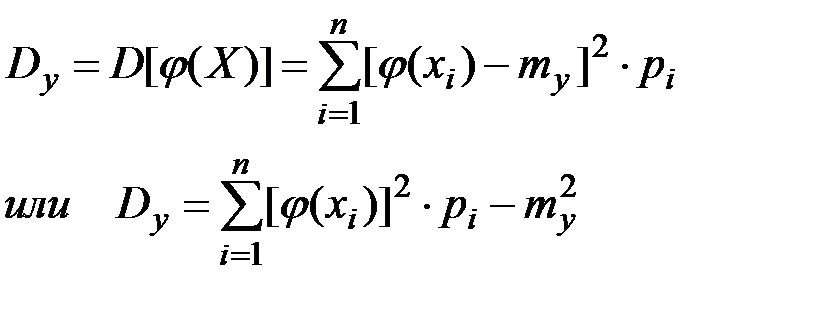 (П2.60)
(П2.60)
Если Х –– непрерывная случайная величина с плотностью распределения f(x), a Y=j(X), то математическое ожидание величины Y равно:
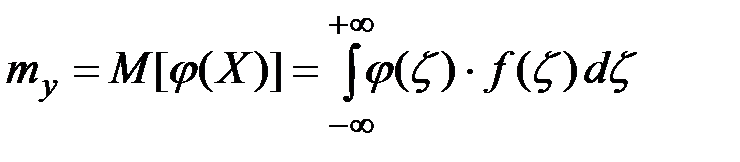 (П2.61)
(П2.61)
Дисперсия определяется с помощью одной из следующих двух формул:
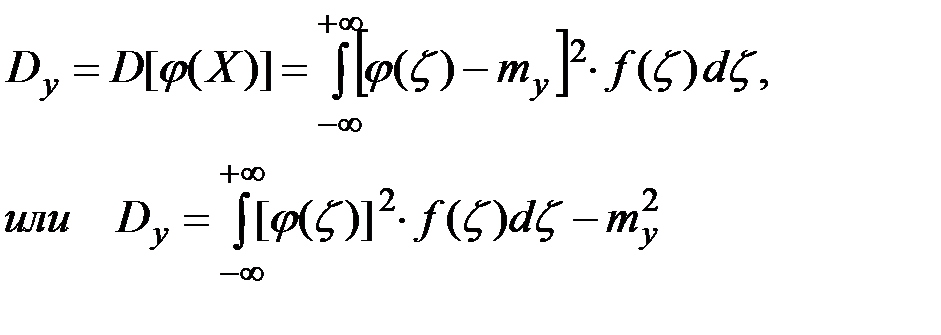
Дата добавления: 2019-02-07; просмотров: 817;
