Некоторые характеристики случайных величин, событий, процессов в оценках надежности технических систем

П2.1. Основные понятия, непосредственный подсчет вероятностей.

Если в результате опыта из общего числа случаев n число благоприятных для события A случаев составляет m, то вероятность реализации события A вычисляется по формуле:

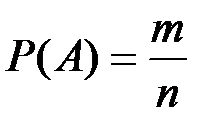(П2.1)
В теории надежности большую роль играет так называемая схема Бернулли. Предположим, что производится последовательно n испытаний, в каждом из которых событие А может произойти с одной и той же вероятностью р. Спрашивается, чему равна вероятность того, что событие А реализуется при m испытаниях, а при n-m испытаниях –– событие не произойдет.

Если обозначить эту вероятность через 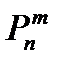, и принять q=1-p, то имеет место формула Бернулли:

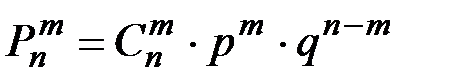(П2.2)
где 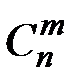–– число сочетаний из n элементов по m.

Наряду с формулой Бернулли значительную роль играет схема, именуемая схемой невозвращенного шара. Если имеется N предметов, среди которых М обладают определенным отличием А, а остальные этим свойством не обладают, то при выборе n единиц наудачу из N предметов, вероятность того, что среди выбранных n предметов m будут отличаться свойством А, определяется формулой:

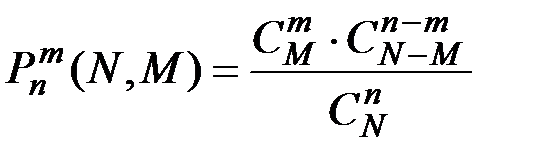(П2.3)

Задача П2.1.

Среди поставленных на испытания элементов имеются a=10 с интенсивностью отказов l=10^-4 1/час и b=6 с интенсивностью отказов l=10^-2 1/час. Эти элементы объединяются в последовательную цепь работы. Найти в среде Matlab надежность системы, собранной из этих элементов, за 2 часа работы.

L1=10^-4;L2=10^-2;t=2;a=10;b=6;

L=a*L1+b*L2;

P=exp(-L*t)

P = 0.8851

Задача П2.2.

В партии, состоящей из 77 изделий, имеется 9 дефектных. Выбирается для контроля 10 изделий. Найти в среде Mathcad вероятность того, что ровно 7 изделий будут с дефектами.

Задача П2.3.

В составе партии, состоящей из 110 изделий, имеется 10% дефектных. Выбирается для контроля 8 изделий. Найти в среде Matlab вероятность того, что ровно 4 изделия будут с дефектами.

k=110;L=110*0.1;r=8;s=4;

PKR=(nchoosek(L,s)*nchoosek(k-L,r-s))/nchoosek(k,r)

PKR = 0.0030; L=11;