Локальна теорема Муавра-Лапласа

Теорема Муавра-Лапласа (локальна). Нехай проводиться n незалежних випробувань, у кожному з яких може з’явитися з імовірністю р деяка подія А. Імовірність того, що подія А відбудеться рівно 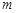разів наближено дорівнює

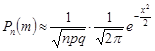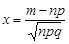, де . (26.7)

Доведення. Імовірність 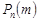можна наближено обчислити за формулою (26.5), якщо взяти 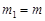та 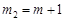. Маємо

,

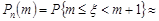
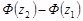де 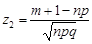і 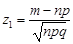. При малих 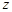маємо

,

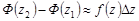де 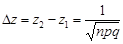, функція 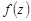– щільність стандартної нормально розподіленої випадкової величини 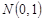, тобто .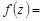

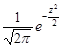Зауважимо, що при малих значеннях 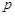та достатньо великих 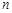знаходження 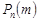за формулою (26.7) дає значну похибку. У цьому випадку застосовують більш точну оцінку, яку дає асимптотична формула Пуассона (8.3).

Приклад 26.3. Завод випускає 80 % продукції першого сорту та 20 % – другого. Яка ймовірність того, що серед навмання відібраних 400 виробів буде 84 виробів другого сорту?

Розв’язання. За умовою задачі 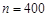, , 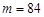ймовірність випуску продукції другого сорту 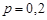, відповідно 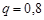. Згідно формулі (26.7) обчислимо

.

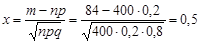За формулою (26.7)

.

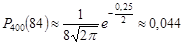Розглянемо приклад, в якому треба віддати перевагу асимптотичній формулі Пуассона.

Приклад 26.4. Імовірність виготовлення бракованого виробу дорівнює 0,002. Яка ймовірність того, що з партії з 1000 навмання взятих виробів, 4 виробу будуть браковані?

Розв’язання. За умовою задачі , , 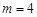ймовірність випуску бракованого виробу 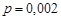, відповідно . Для застосування асимптотичної формули Пуассона (8.3) знаходимо 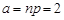. Отже,

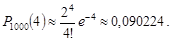
Для асимптотичної формули Муавра-Лапласа обчислимо 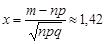. Отже, за формулою (26.7) маємо

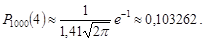
Як бачимо, результати відрізняються один від одного. Оскільки, значення 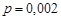мале, а достатньо велике, то перевагу слід віддати результату, який знайдено за формулою Пуассона.

На закінчення зауважимо, що швидкість збіжності до нормального закону при використанні центральної граничної теореми суттєво залежить від типу розподілу доданків у сумі 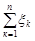. Так, якщо додаються рівномірно розподілені випадкові величини, вже 6 – 9 доданків дають розподіл достатньо близький до нормального. У той же час, щоб досягти таку ж саму близькість при додаванні 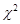розподілених випадкових величин, треба взяти більше 100 доданків.