Локальная и интегральная теоремы Муавра- Лапласа
В тех случаях, когда число испытаний п велико, а вероятность р не близка к нулю (р≠0, р≠1), для вычисления биномиальных вероятностей используют теоремы Муавра-Лапласа. В силу сложности доказательства, приведем только их формулировки.
Теорема 4.3 (Локальная теорема Муавра-Лапласа). Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, а число независимых испытаний достаточно велико, то вероятность 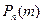 может быть вычислена по приближенной формуле:
может быть вычислена по приближенной формуле:
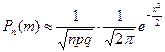 , где , где 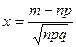 . .
| (4.8) |
Равенство тем точнее, чем больше n.
Выражение 
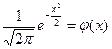
| (4.9) |
называется функцией Гуасса, а ее график – кривой вероятности(рис 4.2).
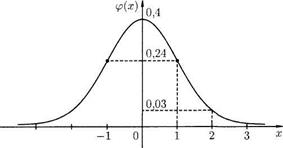
Рис. 4.2.
Равенство (4.8) можно переписать в виде:
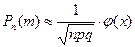 , где , где 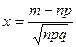 . .
| (4.10) |
Для функции 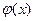 составлены таблицы значений (они находятся, как правило, в так называемая «Приложениях» книг по теории вероятностей). Пользуясь таблицей, следует учитывать, что:
составлены таблицы значений (они находятся, как правило, в так называемая «Приложениях» книг по теории вероятностей). Пользуясь таблицей, следует учитывать, что:
а) функция 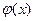 четная, т. е.
четная, т. е. 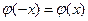
б) при х ≥ 4 можно считать, что 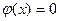 .
.
Пример 4.4.Вероятность попадания в мишень при одном выстреле для данного стрелка равна 0,7. Найти вероятность того, что при 200 выстрелах мишень будет поражена 160 раз.
Решение:
Здесь 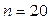 ,
, 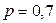 ,
, 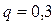 ,
, 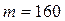 . Применим формулу (4.10).
. Применим формулу (4.10).
Имеем
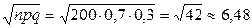 ,
,
следовательно,
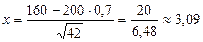 .
.
Учитывая, что 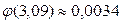 , получаем
, получаем
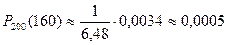 .
.
Теорема 4.4. (Интегральная теорема Муавра-Лапласа). Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность 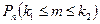 может быть найдена по приближенной формуле:
может быть найдена по приближенной формуле:
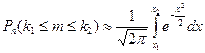 , где , где 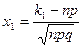 , , 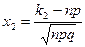 . .
| (4.11) |
Используя функцию Гаусса (4.9), равенство можно записать в виде:
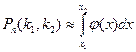 .
.
Однако, для упрощения вычислений вводят специальную функцию:
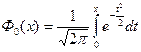 , ,
| (4.12) |
называемую нормированной функцией Лапласа.
Функция (4.12) нечетна
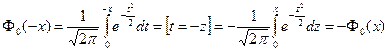 ,
,
при х≥5 можно считать, что 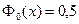 .
.
Если выразить правую часть равенства (4.11) через функцию Лапласа (4.12), тот равенство (4.11) примет вид
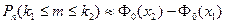 , где , где 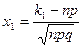 , , 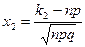 . .
| (4.13) |
Наряду с нормированной функцией Лапласа используют функцию:
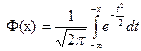 , ,
| (4.14) |
называемую также функцией Лапласа . Для нее справедливо равенство 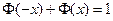 ; она связана с функцией
; она связана с функцией 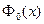 формулой:
формулой:
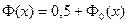 . .
| (4.15) |
Приближенную формулу для вычисления вероятности 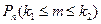 (4.11) можно записать в виде
(4.11) можно записать в виде
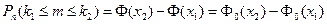 ,
где ,
где 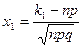 , , 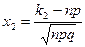 . .
| (4.16 |
Пример 4.5. Проверкой установлено, что цех в среднем выпускает 96% продукции высшего сорта. На базе приемщик проверяет 200 изделий этого цеха. Если среди них окажется более 10 изделий не высшего сорта, то вся партия изделий бракуется, т.е. возвращается в цех. Какова вероятность того, что партия будет принята?
Решение:
Здесь 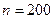 ,
, 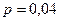 (вероятность негодного изделия),
(вероятность негодного изделия), 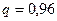 . Вероятность принятия всей партии, т.е.
. Вероятность принятия всей партии, т.е. 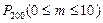 , можно найти по формуле (4.16); здесь
, можно найти по формуле (4.16); здесь 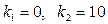 . Находим, что
. Находим, что
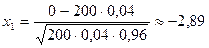 ,
, 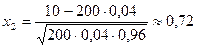 ,
,
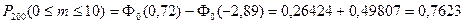 .
.
Заметим, что 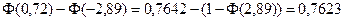 .
.
Дата добавления: 2017-03-29; просмотров: 460;
