Дискретне перетворення Лапласа і частотні характеристики

Дискретним перетворенням Лапласа називають співвідношення

,

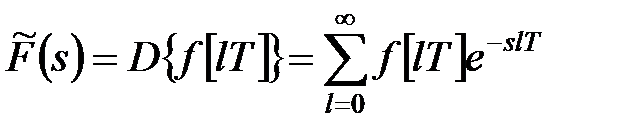що ставить гратчастій функції 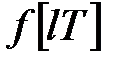у відповідність функцію 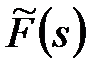комплексного змінного 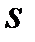. Функцію 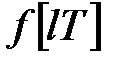називають оригіналом, а 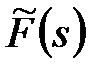– зображенням або 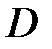-зображенням. Дискретне перетворення виходить з 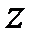-перетворення при підстановці в нього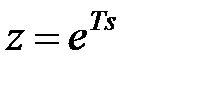

.

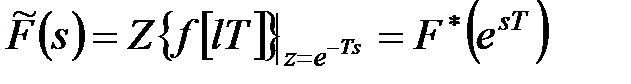Зворотне дискретне перетворення Лапласа має вигляд

.

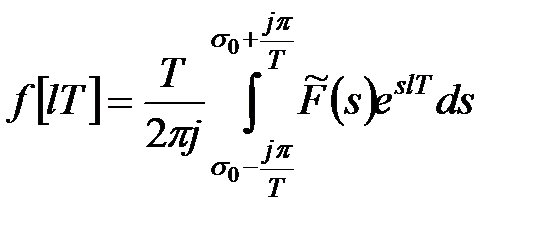(21.8)

Передаточну функцію в дискретних перетвореннях Лапласа або в 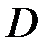-зображеннях 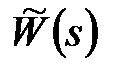можна визначити як дискретне перетворення Лапласа від вагової функції :

.

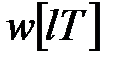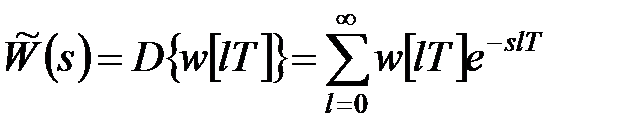Вона пов'язана з передаточною функцією в 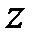-зображеннях співвідношенням

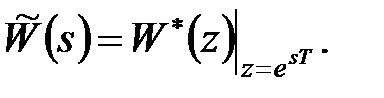
Частотною передаточною функцією (дискретною) називається функція, яка виходить при підстановці в передаточну функцію в 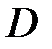-зображеннях :

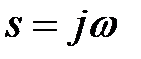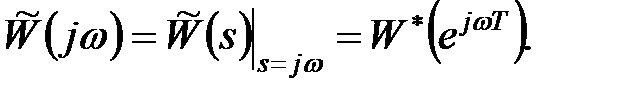
На основі цієї функції точно так, як і у разі безперервних систем, визначаються амплитудно-фазові, амплітудні, фазові і інші частотні функції і їх характеристики.

Оскільки 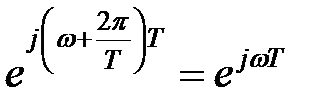, то частотна передаточна функція 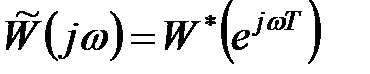є періодичною функцією з періодом 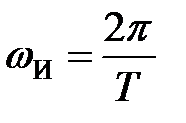Тому при побудові частотних характеристик дискретних систем обмежуються частотами з інтервалу 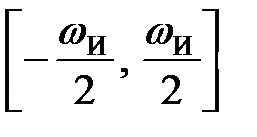або .

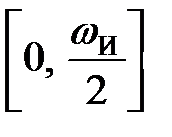Дискретні частотні функції мають такий же фізичний сенс, що і безперервні: якщо на вхід дискретної системи подається гармонійний сигнал 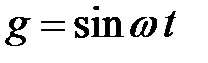то на її виході в сталому режимі в дискретні моменти часу 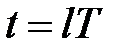будемо мати 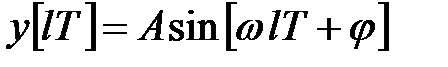. Амплітуда і фаза цього процесу відповідно рівні модулю і аргументу частотної передаточної функції.