Характеристичне рівняння і основна умова стійкості

Якщо зовнішні дії задані, то рівняння дискретної системи управління можна записати у вигляді

.

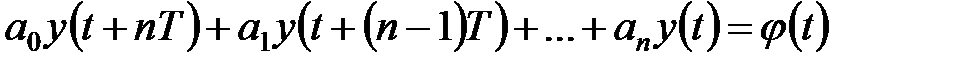(22.1)

або, в операторній формі

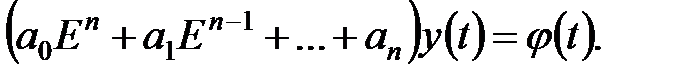
Характеристичне рівняння має вигляд:

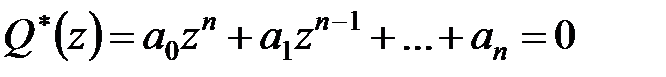
(22.2)

Характеристичний поліном (ліва частина характеристичного рівняння) виходить при підстановці у власного оператора замість оператора зсуву 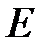змінної .

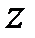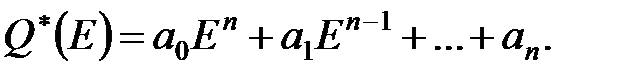
Якщо задана передаточна функція системи управління, то при визначенні характеристичного полінома потрібно виходити з наступних положень: за визначенням передаточної функції в операторній формі її знаменник є власний оператор, а знаменник передаточної функції в 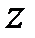-зображеннях співпадає з характеристичним поліномом (за умови, що передаточна функція в операторній формі не містить однакових нулів і полюсів).

Загальне розв’язання неоднорідного різницевого рівняння (22.1) має вигляд

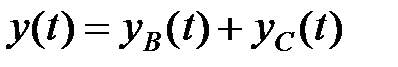
де 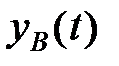– частинне вирішення цього рівняння і 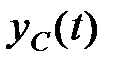– загальне вирішення відповідного однорідного рівняння.

Лінійна дискретна система управління називається стійкою, якщо загальне вирішення однорідного різницевого рівняння при 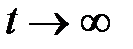прагне до нуля:

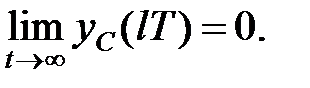
(22.3)

Якщо всі корені 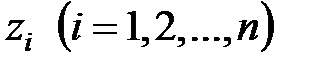характеристичного рівняння прості (тобто різні), то загальне вирішення однорідного різницевого рівняння має вигляд

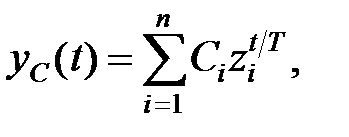
(22.4)

де 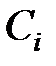– довільні постійні. Якщо серед коренів характеристичного рівняння є кратний корінь 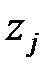кратності 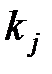то йому в (22.4) відповідає доданок

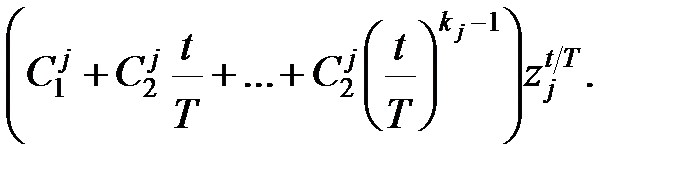
З (22.4) і останнього виразу витікає, що умова (22.3) буде виконана в тому і лише тому випадку, коли 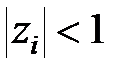при всіх .

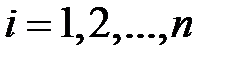Основна умова стійкості. Для того, щоб лінійна дискретна система управління була стійка, необхідно і достатньо, щоб все корені її характеристичного рівняння були по модулю менше одиниці, або, що те ж, знаходилися усередині одиничного круга на 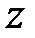-площини.

Приклад 22.1. Передаточна функція системи .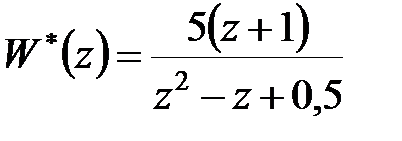

Потрібно дослідити її стійкість.

Рішення. Характеристичне рівняння має вигляд .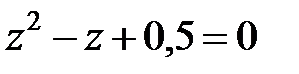

Його коренями являються 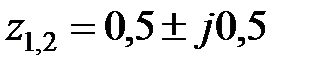. Їх модулі 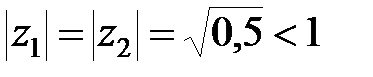. Система стійка.